对数正态分布(logarithmic normal distribution):一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布。
对数正态分布_对数正态分布 -概述
在分析测试中,特别是在衡量分析中,在不少情况下,测定值不遵循正态分布,而是遵循对数正态分布。对数正态分布_对数正态分布 -基本定义
在概率论与统计学中,对数正态分布是对数为正态分布的任意随机变量的概率分布。如果X是服从正态分布的随机变量,则exp(X)服从对数正态分布;同样,如果Y服从对数正态分布,则ln(Y)服从正态分布。如果一个变量可以看作是许多很小独立因子的乘积,则这个变量可以看作是对数正态分布。一个典型的例子是股票投资的长期收益率,它可以看作是每天收益率的乘积。
设ξ服从对数正态分布,其密度函数为:
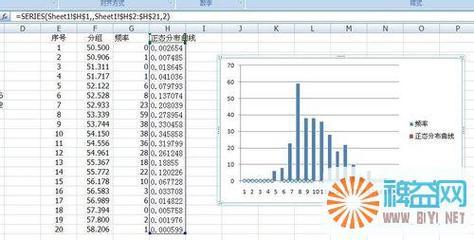
图示
对数正态分布_对数正态分布 -"对数正态分布"在工具书中的解释
1、一些正偏态资料的变量值,通过对数转换后,由偏态分布转为正态分布。某些正偏态资料,如血铅含量、某些传染病的潜伏期等,经对数变换后可符合正态分布。
对数正态分布_对数正态分布 -图片
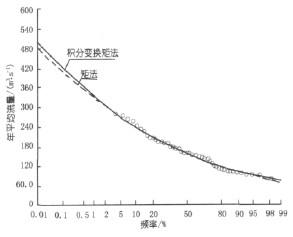
对数正态分布_对数正态分布 -主要学者
王玲玲 王蓉华费鹤良成邦文陈舜华何基报陶然李 斌张志华
陈文华
对数正态分布_对数正态分布 -相关关系
对数正态分布、几何平均数与几何标准差是相互关联的。在这种情况下,几何平均值等于exp(μ),几何
平均差等于exp(σ)。
如果采样数据来自于对数正态分布,则几何平均值与几何标准差可以用于估计置信区间,就像用算术平均数与标准差估计正态分布的置信区间一样。
 爱华网
爱华网