洛伦兹力是从阴极发射出来的电子束,在阴极和阳极间的高电压作用下,轰击到长条形的荧光屏上激发出荧光,可以在示波器上显示出电子束运动的径迹。实验表明,在没有外磁场时,电子束是沿直线前进的,如果把射线管放在蹄形磁铁的两极间,荧光屏上显示的电子束运动的径迹就发生了弯曲,这表明,运动电荷确实受到了磁场的作用力,这个力通常叫做洛伦兹力,它为荷兰物理学家H.A.洛伦兹首先提出,故得名。
洛伦兹力_洛伦兹力 -定义
运动电荷在磁场中所受的力。它是荷兰物理学家H・A・洛伦兹于1895年建立经典电子论时,作为基本假定而提出的,后被大量实验结果所证实,因此得名。
洛伦兹力_洛伦兹力 -公式推导
安培力是洛伦兹力的宏观表现,故从安培力大小公式,可以反推得洛伦兹力公式。
1、从宏观到微观
安培力F=BIL
电流I=Q/t
代入上式F=BL(Q/t)=QvB(从宏观到微观)
2、从微观到宏观
F=BIL=BnqsvL=NBqv
即F(安培力)=Nf (f是洛伦兹力)
3、其它推导
如图2:
图2
洛伦兹力_洛伦兹力 -详解
在电动力学里,洛伦兹力(Lorentz force)是运动于电磁场的带电粒子所受的力。根据洛伦兹力定律,洛伦兹力可以用方程,称为洛伦兹力方程,表达为
洛伦兹力
其中, F是洛伦兹力, q是带电粒子的电荷量,E是电场强度, v是带电粒子的速度, B是磁感应强度。
洛伦兹力定律是一个基本公理,不是从别的理论推导出来的定律,而是由多次重复完成的实验所得到的同样的结果。
感受到电场的作用,正电荷会朝着电场的方向加速;但是感受到磁场的作用,按照左手定则,正电荷会朝着垂直于速度V和磁场B的方向弯曲(详细地说,应用左手定则,当四指指电流方向,磁感线穿过手心时,大拇指方向为洛伦兹力方向)。
洛伦兹力
洛伦兹力方程的qE项是电场力项,
项是磁场力项。
处于磁场内的载电导线感受到的磁场力就是这洛伦兹力的磁场力分量。
洛伦兹力方程的积分形式为
洛伦兹力
其中,V是积分的体积,p是电荷密度,J是电流密度,dr是微小体元素。
经常使用的公式还有洛伦兹力密度f的表达式
洛伦兹力
。
若带电粒子射入匀强磁场内,它的速度与磁场间夹角为0
洛伦兹力
洛伦兹力
洛伦兹力
洛伦兹力
1895年荷兰物理学家H.A.洛伦兹建立经典电子论时,作为基本假设提出来的,现已为大量实验证实。洛伦兹力的公式为
。适用条件:磁场是匀强磁场,v与B方向垂直。式中q、v分别是点电荷的电量和速度,B是点电荷所在处的磁感应强度。v与B方向不垂直时,洛伦兹力的大小是
,其中θ是v和B的夹角。洛伦兹力的方向循左手定则(左手平展,使大拇指与其余四指垂直,并且都跟手掌在一个平面内;把左手放入磁场中,让磁感线垂直穿入手心(手心对准 N极,手背对准S极,四指指向电流方向(即正电荷运动的方向v),则拇指的方向就是导体或正电荷受力方向)垂直于v和B构成的平面(若q为负电荷,则反向)。由于洛伦兹力始终垂直于电荷的速度方向和磁场方向确定的平面,所以它对电荷不作功,不改变运动电荷的速率和动能,只能改变电荷的运动方向使之偏转。
洛伦兹力既适用于宏观电荷,也适用于微观电荷粒子。电流元在磁场中所受安培力就是其中运动电荷所受洛伦兹力的宏观表现。导体回路在恒定磁场中运动,使其中磁通量变化而产生的动生电动势也是洛伦兹力的结果,洛伦兹力是产生动生电动势的非静电力。
洛伦兹力
如果电场E和磁场B并存,则运动点电荷受力为电场力和磁场力之和,为
。
【注】公式中E、B为矢量,右式一般也称为洛伦兹力公式。
洛伦兹力公式和麦克斯韦方程组以及介质方程一起构成了经典电动力学的基础。在许多科学仪器和工业设备,例如β谱仪,质谱仪,粒子加速器,电子显微镜,磁镜装置,霍尔器件中,洛伦兹力都有广泛应用。
值得指出的是,既然安培力是洛伦兹力的宏观表现,洛伦兹力对运动电荷不作功,何以安培力能对载流导线作功呢?实际上洛伦兹力起了传递能量的作用,当导线运动的时候,洛伦兹力的一部分指向电荷运动的反方向,阻碍电荷运动作负功,形成动生电动势;另一部分构成安培力,对载流导线作正功,结果仍是由平衡动生电动势,维持电流的电源提供了能量。
安培力是洛伦兹力的宏观表现,故从安培力大小公式,可以反推得洛伦兹力公式。
1、从宏观到微观
洛伦兹力
安培力
洛伦兹力
电流
洛伦兹力
代入上式
2、从微观到宏观
洛伦兹力
即F(安培力)=Nf (f是洛伦兹力)
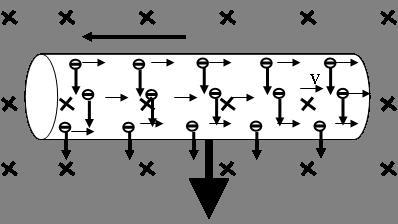
3、其它推导
洛伦兹力
洛伦兹力
洛伦兹力
 爱华网
爱华网