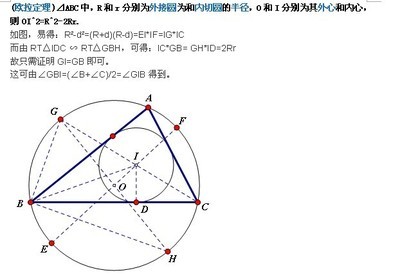
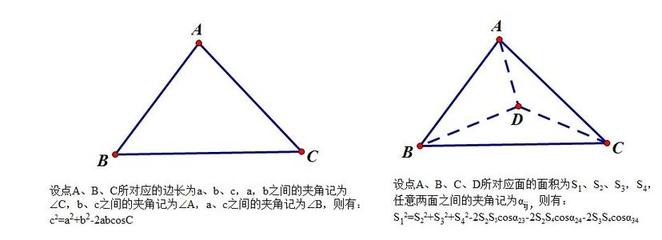
外心是数学名词。指三角形三条边的垂直平分线(中垂线)的相交点。用这个点做圆心可以画三角形的外接圆。外心的性质:三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。计算外心的重心坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。外心到三顶点的距离相等。
外心_外心 -简介
外心数学名词。指三角形三条边的垂直平分线(中垂线)的相交点。用这个点做圆心可以画三角形的外接圆。
指三角形外接圆的圆心,一般叫三角形的外心。三角形的外心是三边中垂线的交点,且这点到三角形三顶点的距离相等。
外心是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心_外心 -相关定理
外心外心定理:三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
证明
注意到外心到三角形的三个顶点距离相等,结合垂直平分线定义,外心定理其实极好证。
计算外心的重心坐标是一件麻烦的事。先计算下列临时变量:
d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:((c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c)。
且:
直角三角形外心在斜边的中点。
锐角三角形外心在内部。
钝角三角形外心在外部。
设O是三角形ABC的外心则∠AOC=2∠ABC,∠AOB=2∠ACB
与多边形各角都相交的圆叫做多边型的外接圆。
三角形一定有外接圆,其他的图形不一定有外接圆。
三角形的外接圆圆心是三条中垂线的交点,直角三角形的外接圆圆心在斜边的中点上。
三角形外接圆圆心叫外心
有外心的图形,一定有外接圆(各边中垂线的交点,叫做外心)
例题分析
例1如图1-125,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-PA-C的平面角的正切值.
分析由PC⊥平面ABC,知平面ABC⊥平面PAC,从而B在平面PAC上的射影在AC上,由此可用三垂线定理作出二面角的平面角.
解∵PC⊥平面ABC
∴平面PAC⊥平面ABC,交线为AC作BD⊥AC于D点,据面面垂直性质定理,BD⊥平面PAC,作DE⊥PA于E,连BE,据三垂线定理,则BE⊥PA,从而∠BED是二面角B-PA-C的平面角.
设PC=a,依题意知三角形ABC是边长为a的正三角形,∴D是
∵PC=CA=a,∠PCA=90°,∴∠PAC=45°∴在Rt△DEA
评注本题解法使用了三垂线定理来作出二面角的平面角后,再用解三角形的方法来求解.
例2在60°二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求点P到直线a的距离.(图1-126)
分析设PA、PB分别为点P到平面M、N的距离,过PA、PB作平面α,分别交M、N于AQ、BQ.
同理,有PB⊥a,
∵PA∩PB=P,
∴a⊥面PAQB于Q
又AQ、BQ
平面PAQB
∴AQ⊥a,BQ⊥a.
∴∠AQB是二面角M-a-N的平面角.
∴∠AQB=60°
连PQ,则PQ是P到a的距离,在平面图形PAQB中,有
∠PAQ=∠PBQ=90°
∴P、A、Q、B四点共圆,且PQ是四边形PAQB的外接圆的直径2R
在△PAB中,∵PA=1,PB=2,∠BPA=180°-60°=120°,由余弦定理得
AB2=1+4-2×1×2cos120°=7
由正弦定理:
评注本例题中,通过作二面角的棱的垂面,找到二面角的平面角.
例3如图1-127过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a求(1)二面角B-PC-D的大小;(2)平面PAB和平面PCD所成二面角的大小.
分析二面角B-PC-D的棱为PC,所以找平面角作棱的垂线,而平面PAB和平面PCD所成二面角“无棱”须找二面角的棱.
解(1)∵PA⊥平面ABCD,BD⊥AC
∴BD⊥PC(三垂线定理)
在平面PBC内,作BE⊥PC,E为垂足,连结DE,得PC⊥平面BED,从而DE⊥PC,即∠BED是二面角B-PC-D的平面角.
在Rt△PAB中,由PA=AB=a
∵PA⊥平面ABCD,BC⊥AB
∴BC⊥PB(三垂线定理)
在Rt△PBC中,
在△BDE中,根据余弦定理,得
∴∠BED=120°
即二面角B-PC-D的大小为120°.
(2)过P作PQ∥AB,则PQ
平面PAB,
∵AB∥CD∴PQ∥CD,PQ
平面PCD
∴平面PAB∩平面PCD于PQ
∵PA⊥AB,AB∥PQ∴PA⊥PQ
∵PA⊥平面ABCD,CD⊥AD
∴CD⊥PD(三垂线定理的逆定理)
∵PQ∥CD∴PD⊥PQ
所以∠APD是平面PAB和平面PCD所成的二面角的平面角.
∵PA=AB=AD,∴∠APD=45°
即平面PAB和平面PCD所成的二面角为45°.
评注在求无棱二面角的大小时有时须作出棱线后再找平面角.
外心_外心 -性质
1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。 2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。4、计算外心的重心坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。重心坐标:((c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c)。5、外心到三顶点的距离相等。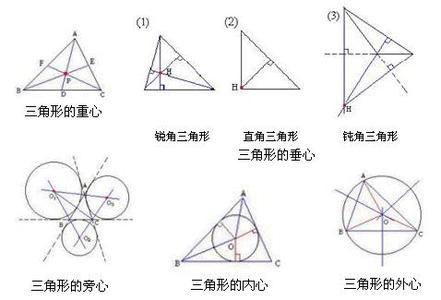
 爱华网
爱华网