复数的历史 复数 复数-历史，复数-主要内容

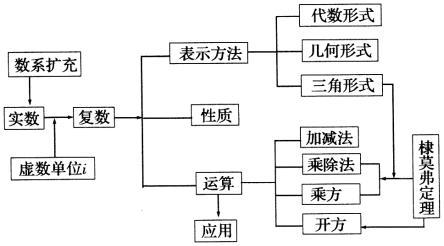
复数是指能写成如下形式的数a+bi,这里a和b是实数，i是虚数单位(即-1开根)。在复数a+bi中，a称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。由上可知，复数集包含了实数集，因而是实数集的扩张。复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

复数（complexnumber）为，形如a＋bi的数。式中a，b为实数，i是一个满足i2＝－1的数，因为任何实数的平方不等于－1，所以i不是实数，而是实数以外的新的数。在复数a＋bi中，a称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。由上可知，复数集包含了实数集，因而是实数集的扩张。

复数公式_复数 -历史

最早有关复数方根的文献出于公元1世纪希腊数学家海伦，他考虑的是平顶金字塔不可能问题。
16世纪意大利米兰学者卡当（JeromeCardan1501―1576）在1545年发表的《重要的艺术》一书中，公布了三次方程的一般解法，被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家，并且在讨论是否可能把10分成两部分，使它们的乘积等于40时，他把答案写成

尽管他认为和这两个表示式是没有意义的、想象的、虚无飘渺的，但他还是把10分成了两部分，并使它们的乘积等于40。给出“虚数”这一名称的是法国数学家笛卡尔（1596―1650），他在《几何学》（1637年发表）中使“虚的数”与“实的数”相对应，从此，虚数才流传开来。
数系中发现一颗新星――虚数，于是引起了数学界的一片困惑，很多大数学家都不承认虚数。德国数学家莱布尼茨（1646―1716）在1702年说：“虚数是神灵遁迹的精微而奇异的隐避所，它大概是存在和虚妄两界中的两栖物”。瑞士数学大师欧拉（1707―1783）说：“一切形如，的数学式子都是不可能有的，想象的数，因为它们所表示的是负数的平方根。对于这类数，我们只能断言，它们既不是什么都不是，也不比什么都不是多些什么，更不比什么都不是少些什么，它们纯属虚幻。”然而，真理性的东西一定可以经得住时间和空间的考验，最终占有自己的一席之地。法国数学家达朗贝尔（1717―1783）在1747年指出，如果按照多项式的四则运算规则对虚数进行运算，那么它的结果总是的形式（a、b都是实数）。法国数学家棣莫弗（1667―1754）在1730年发现了著名的棣莫佛定理。欧拉在1748年发现了有名的关系式，并且是他在《微分公式》（1777年）一文中第一次用i来表示-1的平方根，首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的，而它是确实存在的。挪威的测量学家成塞尔（1745―1818）在1779年试图给于这种虚数以直观的几何解释，并首先发表其作法，然而没有得到学术界的重视。
十八世纪末，复数渐渐被大多数人接受，当时卡斯帕尔・韦塞尔提出复数可看作平面上的一点。数年后，高斯再提出此观点并大力推广，复数的研究开始高速发展。诧异的是，早于1685年约翰・沃利斯已经在DeAlgebratractatus提出此一观点。
卡斯帕尔・韦塞尔的文章发表在1799年的ProceedingsoftheCopenhagenAcademy上，以当今标准来看，也是相当清楚和完备。他又考虑球体，得出四元数并以此提出完备的球面三角学理论。1804年，AbbéBuée亦独立地提出与沃利斯相似的观点，即以来表示平面上与实轴垂直的单位线段。1806年，Buée的文章正式刊出，同年让-罗贝尔・阿尔冈亦发表同类文章，而阿冈的复平面成了标准。1831年高斯认为复数不够普及，次年他发表了一篇备忘录，奠定复数在数学的地位。柯西及阿贝尔的努力，扫除了复数使用的最后顾忌，后者更是首位以复数研究著名的。
复数吸引了著名数学家的注意，包括库默尔（1844年）、克罗内克（1845年）、Scheffler（1845年、1851年、1880年）、Bellavitis（1835年、1852年）、乔治・皮库克（1845年）及德・摩根（1849年）。莫比乌斯发表了大量有关复数几何的短文，约翰・彼得・狄利克雷将很多实数概念，例如素数，推广至复数。
德国数学家阿甘得（1777―1855）在1806年公布了虚数的图象表示法，即所有实数能用一条数轴表示，同样，虚数也能用一个平面上的点来表示。在直角坐标系中，横轴上取对应实数a的点A，纵轴上取对应实数b的点B，并过这两点引平行于坐标轴的直线，它们的交点C就表示复数。象这样，由各点都对应复数的平面叫做“复平面”，后来又称“阿甘得平面”。高斯在1831年，用实数组代表复数，并建立了复数的某些运算，使得复数的某些运算也象实数一样地“代数化”。他又在1832年第一次提出了“复数”这个名词，还将表示平面上同一点的两种不同方法――直角坐标法和极坐标法加以综合。统一于表示同一复数的代数式和三角式两种形式中，并把数轴上的点与实数一一对应，扩展为平面上的点与复数一一对应。高斯不仅把复数看作平面上的点，而且还看作是一种向量，并利用复数与向量之间一一对应的关系，阐述了复数的几何加法与乘法。至此，复数理论才比较完整和系统地建立起来了。
经过许多数学家长期不懈的努力，深刻探讨并发展了复数理论，才使得在数学领域游荡了200年的幽灵――虚数揭去了神秘的面纱，显现出它的本来面目，原来虚数不“虚”。虚数成为了数系大家庭中一员，从而实数集才扩充到了复数集。
随着科学和技术的进步，复数理论已越来越显出它的重要性，它不但对于数学本身的发展有着极其重要的意义，而且为证明机翼上升力的基本定理起到了重要作用，并在解决堤坝渗水的问题中显示了它的威力，也为建立巨大水电站提供了重要的理论依据。

复数公式_复数 -主要内容

形式

数集拓展到实数范围内，仍有些运算无法进行。比如判别式小于0的一元二次方程仍无解，因此将数集再次扩充，达到复数范围。
形如z=a+bi的数称为复数（complexnumber)，其中规定i为虚数单位，且i2=i×i=－1（a，b是任意实数）
我们将复数z=a+bi中的实数a称为复数z的实部（realpart)记作Rez=a

实数b称为复数z的虚部（imaginarypart）记作Imz=b.
已知：当b=0时，z=a，这时复数成为实数；当且仅当a=b=0时，它是实数0；
当a=0且b≠0时，z=bi，我们就将其称为纯虚数。

复数的模

将复数的实部与虚部的平方和的正的平方根的值称为该复数的模，记作

爱华网本文地址 » http://www.aihuau.com/a/8104070103/169958.html