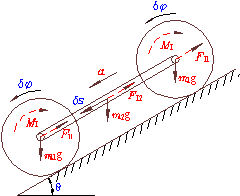
单摆Simple pendulum,是由一根不会伸缩的细线或细棒和一个很小的重球所构成的振动系统。用一根绝对挠性且长度不变、质量可忽略不计的线悬挂一个质点,在重力作用下在铅垂平面内作周期运动,就成为单摆。单摆在摆角小于5°(现在一般认为是小于10°)的条件下振动时,可近似认为是简谐运动。单摆运动的周期公式:T=2π√(L/g).其中L指摆长,g是当地重力加速度。
单摆_单摆 -简介
周期
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关。公式
单摆是一种理想的物理模型,它由理想化的摆球和摆线组成.摆线由质量不计、不可伸缩的细线提供;摆球密度较大,而且球的半径比摆线的长度小得多,这样才可以将摆球看做质点,由摆线和摆球构成单摆.在满足偏角<10°的条件下,单摆的周期:
从公式中可看出,单摆周期与振幅和摆球质量无关.从受力角度分析,单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力,偏角越大,回复力越大,加速度(gsin)越大,在相等时间内走过的弧长也越大,所以周期与振幅、质量无关,只与摆长l和重力加速度g有关.在有些振动系统中l不一定是绳长,g也不一定为9.8m/s,因此出现了等效摆长和等效重力加速度的问题.
单摆
物理上有些问题与单摆类似,经过一些等效可以套用单摆的周期公式,这类问题称为“等效单摆”.等效单摆在生活中比较常见.除等效单摆外,单摆模型在其他问题中也有应用.
说明
质点振动系统的一种,是最简单的摆。绕一个悬点来回摆动的物体,都称为摆,但其周期一般和物体的形状、大小及密度的分布有关。但若把尺寸很小的质块悬于一端固定的长度为l且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所成角度小于10°,放手后质块往复振动,可视为质点的振动,其周期T只和l和当地的重力加速度g有关,即而和质块的质量、形状和振幅的大小都无关系,其运动状态可用简谐振动公式表示,称为单摆或数学摆。如果振动的角度大于10°,则振动的周期将随振幅的增加而变大,就不成为单摆了。如摆球的尺寸相当大,绳的质量不能忽略,就成为复摆(物理摆),周期就和摆球的尺寸有关了。首先由牛顿力学,单摆的运动可作如下描述:
单摆_单摆 -动力学方程
首先我们可以得到,
其中m为质量,g是重力加速度,l是摆长,θ是单摆与竖直方向的夹角,注意,θ是矢量,这里取它在正方向上的投影。
我们希望得到摆角θ的关于时间的函数,来描述单摆运动。由角动量定理我们知道,
其中
是单摆的转动惯量,
是角加速度。于是化简得到
(1)
单摆_单摆 -小角度近似周期
我们知道(1)式是一个非线性微分方程。所以严格地说上面的(1)式描述的单摆的运动并不是简谐运动。
不过,在θ比较小时,近似地有sinθ≈θ。(即
。)因而此时(1)式就变为
,这是一个二阶常系数线性齐次微分方程,其通解为,式中A.为任意常数,由初值条件给定。而于是单摆的非线性的运动被线性地近似为简谐运动
一般在高考之类的考试中,认为10°以下可以这样近似。
事实上5°≈0.087266弧度,Sin5°≈0.087155,二者相差只有千分之一点几,是十分接近的。在低精度的实验中,这种系统误差可以忽略不计(因为实验操作中的偶然误差就比它大)。但如果换成25°,误差高达百分之三,就不宜再看成是简谐振动了。
由于正弦函数的性质,这个近似是角度越小,越精确,角度越大越不精确。如果角度很大(比如60度处,误差高达17%),就完全不能说它是简谐振动了。
单摆图片
伽利略第一个发现摆的振动的等时性,并用实验求得单摆的周期随长度的二次方根而变动。惠更斯制成了第一个摆钟。单摆不仅是准确测定时间的仪器,也可用来测量重力加速度的变化。惠更斯的同时代人天文学家J.里希尔曾将摆钟从巴黎带到南美洲法属圭亚那,发现每天慢2.5分钟,经过校准,回巴黎时又快2.5分钟。惠更斯就断定这是由于地球自转引起的重力减弱。I.牛顿则用单摆证明物体的重量总是和质量成正比的。直到20世纪中叶,摆依然是重力测量的主要仪器。
单摆_单摆 -真实周期推导
上面提到是角度比较小的时候单摆的近似公式,但科学是严谨的,在此补充在任意角度下单摆的周期公式。
在此之前先提出两个概念(我用mathematica的定义):
第一类不完全椭圆积分:
第一类完全椭圆积分:
下面我用微分方程进行讨论,读者可以尝试用动能定理进行计算,可以更简洁地得到其特解。
设摆长为l,摆线与竖直方向的夹角为θ,那么单摆的运动公式为:
令
,于是有
上式改写成:
这是一个可分离变量的微分方程!分离变量:
其通解为
给定初始条件
(0≤α≤π),,则其特解为:
所以考虑t(t是四分之一周期):
设
,则
又考虑到
便可以化简得到
按照前面的定义,便有
此处的α就是常说的摆角。
单摆_单摆 -近似公式与真实值差别
利用电脑软件,我们列出近似公式与真实公式的差别。
下面数据皆是相对误差:相对误差=(真实值-近似值)/真实值
每一行,摆角相差1度,自0取到180度。
0
0.0019038558531896002%
0.0076153871712633745%
0.01713448526148856%
0.030460969075184717%
0.047594585366650885%
0.06853500891589595%
0.09328184281540482%
0.12183461882124084%
0.1541927977688524%
0.1903557700540208%
0.23032285617945628%
0.27409330736761933%
0.32166630624041737%
0.37304096756649924%
0.42821633907694606%
0.48719140235023334%
0.549965073767417%
0.6165362055385787%
0.686903586801647%
0.7610659447947971%
0.839021946103721%
0.92077019798515%
1.006309249768103%
1.0956375943344412%
1.188753669680396%
1.2856558605608566%
1.386342500218304%
1.490811872198394%
1.599062212254311%
1.7110917103421366%
1.8268985127096076%
1.9464807240807704%
2.0698364099391786%
2.1969635989124314%
2.3278602852610035%
2.4625244314744745%
2.600953970978439%
2.7431468109555626%
2.8891008352844154%
3.038813907599942%
3.192283874479603%
3.3495085687594606%
3.5104858129847005%
3.675213422999331%
3.843689211680047%
4.0159109928195225%
4.191876585164665%
4.371583816615697%
4.555030528592199%
4.742214580572629%
4.933133854814164%
5.127786261260084%
5.326169742642323%
5.5282822797872475%
5.734121897133129%
5.9436866684683%
6.156974722899461%
6.3739842510601274%
6.594713511569824%
6.819160837755173%
7.04732464464473%
7.279203436250061%
7.514795813146305%
7.754100480366246%
7.99711625562274%
8.243842077875229%
8.494277016257039%
8.748420279381131%
9.006271225043092%
9.2678293703413%
9.533094402235417%
9.802066188565687%
10.074744789556986%
10.351130469833013%
10.63122371096772%
10.915025224602775%
11.202535966161768%
11.493757149193899%
11.788690260382037%
12.087337075252421%
12.389699674625776%
12.695780461852351%
13.00558218087636%
13.319107935178396%
13.636361207647948%
13.957345881441757%
14.282066261887804%
14.610527099499105%
14.942733614166162%
15.278691520602091%
15.61840705511994%
15.961887003827869%
16.309138732334322%
16.660170217062607%
17.014990078281997%
17.373607614971124%
17.7360328416386%
18.10227652723615%
18.472350236310504%
18.846266372552723%
19.224038224916786%
19.605680016494205%
19.991206956347447%
20.380635294522822%
20.773982380483087%
21.171266725221678%
21.57250806734433%
21.977727443430435%
22.386947263015642%
22.800191388569722%
23.21748522087999%
23.63885579029045%
24.06433185429185%
24.493944002007527%
24.92772476617582%
25.365708743292277%
25.807932722644754%
26.254435825053335%
26.70525965221522%
27.160448447654655%
27.62004927039044%
28.08411218256101%
28.552690452391587%
29.025840774051932%
29.50362350614023%
29.986102930741776%
30.47334753525516%
30.965430319458193%
31.462429130607322%
31.96442702973461%
32.47151269273426%
32.98378085032637%
33.50133277156177%
34.0242767962028%
34.552728922099824%
35.086813454603366%
35.62666372613477%
36.17242289531702%
36.72424483658309%
37.282295132982576%
37.84675218706157%
38.41780846727546%
38.99567191050804%
39.58056750504079%
40.172739082901636%
40.77245135613077%
41.37999223839477%
41.99567550190461%
42.61984383019676%
43.25287234061159%
43.895172667035965%
44.54719771472042%
45.20944722616039%
45.88247433208869%
46.56689330724679%
47.263388810526784%
47.972726968588255%
48.69576876871157%
49.433486371410815%
50.18698315232789%
50.95751856030661%
51.7465392710714%
52.55571868071775%
53.38700761086381%
54.24270033499423%
55.12552192866632%
56.03874591621829%
56.986355981090206%
57.97327350290041%
59.00568652891076%
60.09154082585585%
61.24130132912596%
62.46918883739732%
63.795307588848516%
65.24958544634976%
66.87982354979094%
68.77058140504862%
71.09802414324294%
74.36597547372776%
100%
单摆_单摆 -精确函数
单摆的角度随时间的变化,用积分的方法无限逼近,可以有精确结果,有电脑程序来执行,误差也可以得到计算,逼近的方法如下,假设角速度为ω,ω=dα/dt,摆角的加速度为dω/dt,根据牛顿定律,L*dω/dt=-g*sin(α),此公式用下列方法积逼近
ω(t)=-Σ√(L/g)sin(α)Δt,当Δt,足够小的时候,ω(t)的值误差就收敛在要求范围内,同样
α(t)=Σ[(ω(t)+ω(t+Δt)]/2Δt(为更快收敛在截取点去平均值)
把Δt不断分割小,用上述公式计算α就会也越来越接近,在一定时间(N个周期)计算的精度误差小于一定值的,则可得到精确结果。
小角近似公式和实际曲线比较
从结果得知,精确的结果和物理书近似公式一样,是一个三角函数(或者无限逼近一个三角函数),只是在最大振幅摆动比较大的时候,周期发生了较大的变化。由下图红线(物理书近似公式)和绿线(计算机逼近积分)可以看到当振幅是60度时,周期的差别。
当最大摆角越大,由简谐震动而来物理书计算公式误差也越大。然而经过计算机模拟,发现单摆运动仍然是简谐运动,只不过频率减慢,或周期加长,频率减慢的幅度单纯是最大振幅角的一个简单函数,与摆长无关。假设摆角为,时间为t,最大摆角是α0,则单摆α随时间变化真正的公式是
α(t)=α0cos(√(g/L)*(1-0.0620315447*α0*α0)*(t-t0))
(此系数0.0620315447应用于α0角是弧度度单位,在-π/2到π/2之间)
或者
α(t)=α0cos(√(g/L)*(1-1.89519687E-05*α0*α0)*(t-t0))
(此系数应用于α0角是角度单位,在-90到90度之间)
经验角速度校正系数近似公式和实际比较
也就是说,当物理书近似公式的摆动频率是ω0=√(L/g)时
在最大摆角为90度范围内,真正的单摆运动仍然非常逼近三角函数,只是真正的频率是近似频率乘以一个简单的二次方函数。
ω=(1-0.0620315447*α0*α0)*ω0=(1-0.0620315447*α0*α0)*√(L/g)
而这个公式,可以在振幅0-85度范围内,误差全部小于0.01%。
这个常数系数0.0620315447是由对于模拟周期测量之后,算出角速度ω,左图随着振幅角度的变化,电脑得出精确函数的角速度ω
与物理书近似公式的角速度ω0的比率ω/ω0,振幅为0度,角速度相等,比率ω/ω0为1,振幅越大,精确的角速度变得越小,ω/ω0也下降,
绿线是从电脑测出的比例,蓝线则是上述经验公式计而得出的比例,两者几乎完全吻合。
振幅为60度时,小角度近似公式与实际对比
与小角振幅近似公式的周期比较得来,为什么是固定常数造成了一个振幅角度的简单二次方函数,为什么是这个数值。图的红色和绿色是上述公式与计算机无限逼近的积分结果的叠和。显示范围在一个周期。全程范围内误差都至少小于0.001%(甚至可能完全精确)
和近似公式相比,大振幅的单摆运动和物理书的近似公式相比,只是摆动周期或者频率发生了变化,其三角函数的性质完全相同。
右图是上述经验公式,与电脑模拟的实际摆动的叠和。也就是说,经过用振幅修正角速度后,两者几乎完全吻合
单摆_单摆 -应用
当单摆周期T=2s时,由公式推导,摆长大约为1m,这种情况的单摆叫做秒摆。秒摆常见于摆钟上。
注意:在当前高中阶段,一般研究摆角小于10°的情况(即近似看做简谐运动),且高中阶段教材中仅涉及在试验中推测公式,不涉及单摆周期公式的推导(因为需要涉及到高等数学)。
 爱华网
爱华网