顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 与圆相切的直线,同圆内弦相交所形成的夹角叫做弦切角。
弦切角定理_弦切角定理 -弦切角定义
弦切角定理
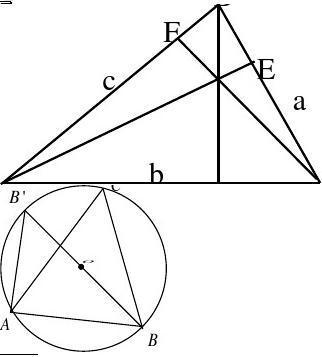
如图所示,线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理_弦切角定理 -弦切角定理
概念及其证明
上图
弦切角定理:弦切角的度数等于它所夹的弧的圆心角度数的一半。
等于它所夹的弧的圆周角度数。
如上图,已知:直线PT切圆O于点C,BC、AC为圆O的弦。
求证:∠TCB=1/2∠BOC=∠BAC
证明:设圆心为O,连接OC,OB,。
∵PC2=PB×AP
∴PC/AP=PB/PC
又∵∠CPB=∠BPC
∴△CAP∽△BCP
∴∠CAP=∠BCP
∴∠TCB=∠BAC
∴∠TCB=1/2∠BOC=∠BAC
综上所述:∠TCB=1/2∠BOC=∠BAC
衍生问题及其证明
已知:AC是⊙O的弦,AB是⊙O的切线,A为切点,弧CmA是弦切角∠BAC所夹的弧.
求证:弦切角∠BAC的度数等于它所夹的弧的度数的一半
弦切角定理
证明:分三种情况:
(1)圆心O在∠BAC的一边AC上
∵AC为直径
∴弧CmA=弧CA
∵弧CA为半圆,
∴弧CmA的度数为180°
∵AB为圆的切线
∴∠CAB=90°
∴弦切角∠BAC的度数等于它所夹的弧的度数的一半
(2)圆心O在∠BAC的内部.
弦切角定理
过A作直径AD交⊙O于D,在优弧m所对的劣弧上取一点E,
连接EC、ED、EA。则
∵弧CD=弧CD
∴∠CED=∠CAD
∵AD是圆O的直径
∴∠DEA=90°
∵AB为圆的切线
∴∠BAD=90°
∴∠DEA=∠BAD
∴ ∠CEA=∠CED+∠DEA=∠CAD+∠BAD=∠BAC
又∠CEA的度数等于弧CmA的度数的一半
∴弦切角∠BAC的度数等于它所夹的弧的度数的一半
弦切角定理
(3)圆心O在∠BAC的外部
过A作直径AD交⊙O于D,连接CD
∵AD是圆的直径
∴∠ACD=90°
∴∠CDA+∠CAD=90°
∵AB是圆O的切线
∴∠DAB=90°
∴∠BAC+∠CAD=90°
∴∠BAC=∠CDA
∵∠CDA的度数等于弧CmA的度数的一半。
∴弦切角∠BAC的度数等于它所夹的弧的度数的一半。
弦切角定理逆定理
定理:以三角形任意一条边为邻边,在三角形外部作一个角等于该边的对角,那么所作角的另一边与三角形外接圆相切,切点为所作角的顶点。
几何描述:设△ABP的外接圆为⊙O,在△ABP外部作∠BAC=∠BPA,则AC切⊙O于A。
注意定理的描述,所作角必须在三角形的外部,且该角与三角形有公共的边。
该定理的等价描述为:角的度数等于所夹弧所对圆周角的角为弦切角。
几何描述:设直线AC与圆相交于A,AB是圆的一条弦,P是圆上与A,B不重合的点。若∠BAC=∠BPA,则∠BAC是弦切角,即AC与圆相切于A。
弦切角定理
证明:如图,同样分类讨论
(1)当∠BPA=90°时,AB为直径。
∠BAC=∠BPA=90°,即AB⊥AC
经过直径的一端,并且与直径垂直的直线是圆的切线,∴AC是⊙O的切线,切点为A。
(2)当∠BPA
∵∠BAC=∠BPA,∠DAB=∠DPB
∴∠BAC+∠DAB=∠BPA+∠DPB
即∠DAC=∠DPA=90°
由(1)得AC与⊙O切于A
(3)当∠BPA>90°时,作直径AD,连接PD,则∠DPA=90°
∵∠BAC=∠BPA,∠BAD=∠BPD
∴∠BAC-∠BAD=∠BPA-∠BPD
即∠DAC=∠DPA=90°
由(1)得AC切⊙O于A
弦切角定理_弦切角定理 -推论
推论内容
若两弦切角所夹的弧相等,则这两个弦切角也相等。
应用举例
弦切角定理
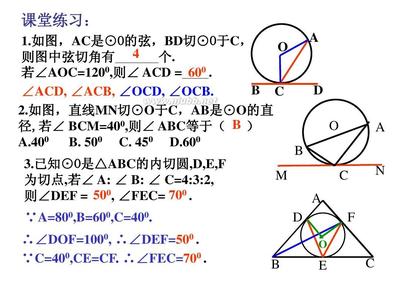
例1:如图,在⊙O中,⊙O的切线AC、BC交于点C,求证:∠CAB=∠CBA。
解:∵AC、BC是⊙O的两条切线,
∴AC=BC(切线长定理)。
∴∠CAB=∠CBA。(等腰三角形“等边对等角”)。
例2:如图,AD是ΔABC中∠BAC的平分线,经过点A的圆与BC相切于点D,与AB,AC分别相交于E,F.
弦切角定理
求证:EF//BC.
证明:连接DF
∵AD是∠BAC的平分线
∴∠BAD=∠CAD
∵∠EFD=∠BAD
∴∠EFD=∠CAD
∵⊙O切BC于D
∴∠FDC=∠CAD
∴∠EFD=∠FDC
∴EF∥BC
弦切角定理
例3:如图,ΔABC内接于⊙O,AB是⊙O直径,CD⊥AB于D,MN切⊙O于C,
求证:AC平分∠MCD,BC平分∠NCD.
证明:∵AB是⊙O直径
∴∠ACB=90
∵CD⊥AB
∴∠A+∠B=∠A+∠DCA
∴∠ACD=∠B,
∵MN切⊙O于C
∴∠MCA=∠B,
∴∠MCA=∠ACD,
即AC平分∠MCD,
同理:BC平分∠NCD。
 爱华网
爱华网