库仑定律适用条件 库仑定律 库仑定律-简介，库仑定律-成立条件

库仑定律的常见表述是：真空中两个静止的点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上，同名电荷相斥，异名电荷相吸。该定律由法国物理学家库仑于1785年在《电力定律》一论文中提出。库仑定律是电学发展史上的第一个定量规律，是电磁学和电磁场理论的基本定律之一。库仑定律没有解决电荷间相互作用力是如何传递的，甚至按照库仑定律的内容，库仑力不需要接触任何媒介，也不需要时间，而是直接从一个带电体作用到另一个带电体上的。

库仑定律_库仑定律 -简介

库仑定律（Coulomb's law），法国物理学家查尔斯・库仑于1785年发现，因而命名的一条物理学定律。库仑定律是电学发展史上的第一个定量规律。因此，电学的研究从定性进入定量阶段，是电学史中的一块重要的里程碑。库仑定律阐明，在真空中两个静止点电荷之间的相互作用力与距离平方成反比，与电量乘积成正比，作用力的方向在它们的连线上，同号电荷相斥，异号电荷相吸。

库仑定律_库仑定律 -成立条件

1.真空中

2.静止

3.点电荷

（静止是在观测者的参考系中静止，中学计算一般不做要求）

库仑定律_库仑定律 -验证

库仑定律是1784--1785年间库仑通过扭秤实验总结出来的。纽秤的结构如下:在细金属丝下悬挂一根秤杆，它的一端有一小球A，另一端有平衡体P，在A旁还置有另一与它一样大小的固定小球B。为了研究带电体之间的作用力，先使A、B各带一定的电荷，这时秤杆会因A端受力而偏转。转动悬丝上端的悬钮，使小球回到原来位置。这时悬丝的扭力矩等于施于小球A上电力的力矩。如果悬丝的扭力矩与扭转角度之间的关系已事先校准、标定，则由旋钮上指针转过的角度读数和已知的秤杆长度，可以得知在此距离下A、B之间的作用力。如何比较力的大小【通过悬丝扭转的角度可以比较力的大小】

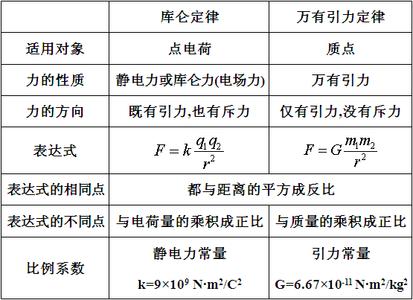
静电学中描述在无限大真空中两个点电荷q1与q2间作用力的定律。是电磁场理论的基本定律之一。它说明q1对于q2的作用力F与它们之间距离r的平方成反比,与电量q1、q2分别成正比。

式中F的单位为牛顿(N),q1和q2的单位为库仑(C),r的单位为米(m)，k为静电常数，ε0称为真空介电常数（k=1/4πε0）

力F的方向沿着两个点电荷q1和q2的连线。两电荷异号时，F为吸力；两电荷同号时，F为斥力。
库仑定律是法国物理学家C.-A.库仑于 1785年通过扭秤实验得出的。他使用扭秤测量了作用力，但当时的实验精度不高。通过间接的方法,可以检验平方反比律中指数2的精确程度。J.C.麦克斯韦得出,若令公式中r的方次为2+δ,δ为误差，则δ的上限为|δ|≤1/21600。1936年，S.J.普林顿和W. E.劳顿通过实验得出：|δ|＜2×10。1971年,E.R.威廉斯、J.E.费勒和H.A.希尔求得δ的极限值为(2.7±3.1)×10 。此外，E.卢瑟福所做的原子核对α粒子散射的实验证明:在带电粒子间近至10cm的核尺度上,库仑定律仍保持有效。但对于比这小的距离,定律则不成立。
如果真空中有多个点电荷，作用于任一点电荷（如q1）上的总力是其他点电荷分别对于q1的作用力的矢量和。两个电荷间的作用力不因其他电荷的存在而改变。
如果q1和q2两个电荷都浸没在一无限大的均匀、各向同性电介质中，ε为电介质的介电常数。空气(0℃，1大气压时)的ε＝1.00059ε0，ε0为真空介电常数。

库仑定律_库仑定律 -公式

COULOMB’SLAW

库仑定律――描述静止点电荷之间的相互作用力的规律真空中，点电荷q1对q2的作用力为

F=k*(q1*q2)/r^2(可结合万有引力公式F=Gm1m2/r^2来考虑）

其中：

r――两者之间的距离

r――从q1到q2方向的矢径

k――库仑常数

上式表示：若q1与q2同号，F12y沿r方向――斥力；

若两者异号，则F12沿-r方向――吸力.

显然q2对q1的作用力

F21=-F12（1-2）

在MKSA单位制中

力F的单位：牛顿（N）=千克・米/秒2(kg・m/S2)（量纲：MLT-2）

电量q的单位：库仑（C）

定义：当流过某曲面的电流1安培时，每秒钟所通过的电量定义为1库仑，即

1库仑（C）=1安培・秒（A・S）（量纲：IT）

比例常数k=1/4pe0(1-3)=9.0x10^9牛・米2/库2

e0=8.854187818(71)×10-12库2/牛・米2(通常表示为法拉/米)

是真空介电常数英文名称：permittivityofvacuum

说明:又称绝对介电常数。符号为εo。等于8.854187817×10-12法/米。它是导自真空磁导率和光在真空中速度的一个无误差常量。

库仑定律_库仑定律 -物理意义

(1)描述点电荷之间的作用力，仅当带电体的尺度远小于两者的平均距离，才可看成点电荷

(2）描述静止电荷之间的作用力，当电荷存在相对运动时，库仑力需要修正为Lorentz力.但实践表明，只要电荷的相对运动速度远小于光速c，库仑定律给出的结果与实际情形很接近。

[例1-1]比较氢原子中质子与电子的库仑力和万有引力（均为距离平方反比力）

据经典理论，基态氢原子中电子的“轨道”半径r≈5.29×10-11米

核子的线度≤10-15米,电子的线度≤10-18米,故两者可看成“点电荷”.

两者的电量e≈±1.60×10-19库仑质量m≈1.67×10-27千克me≈9.11×10-31千克

万有引力常数G≈6.67×10-11牛・米2/千克2

电子所受库仑力Fe=-e2r/4pe0r3电子所受引力Fg=-Gmpmer/r3

两者之比：Fe/Fg=e2/4pe0Gmpme≈2.27×1039（1-6）

由此可见，电磁力在原子、分子结构中起决定性作用，这种作用力远大于万有引力引起的作用力，即可表述为质量对物体间的影响力远小于电磁力的作用，并且有：电荷之间的作用力随着电荷量的增大而增大，随着距离的增大而减小。

库仑定律_库仑定律 -发现

提出

库仑定律可以说是一个实验定律，也可以说是牛顿引力定律在电学和磁学中的“推论”。假如说它是一个实验定律，库仑扭称实验起到了重要作用，而电摆实验则起了决定作用；即便是这样，库仑仍然借鉴了引力理论，模拟万有引力的大小与两物体的质量成正比的关系，认为两电荷之间的作用力与两电荷的电量也成正比关系。假如说它是牛顿万有引力定律的推论，那么普利斯特利和卡文迪许等人也做了大量工作。因此，从各个角度考察库仑定律，重新准确的对它进行熟悉，确实是非常必要的。

电力研究

人类对电现象的熟悉、研究，经历了很长的时间。直到16世纪人们才对电的现象有了深入的熟悉。吉尔伯特比较系统地研究了静电现象，第一个提出了比较系统原始理论，并引人了“电吸引”这个概念。但是吉尔伯特的工作仍停留在定性的阶段，进展不大。18世纪中叶，人们借助于万有引力定律，对电和磁做了种种猜测。18世纪后期，科学家开始了电荷相互作用的研究。

富兰克林最早观察到电荷只分布在导体表面。普利斯特利重复了富兰克林的实验，在《电学的历史和现状》一书中他根据牛顿的《自然哲学的数学原理》最先预言电荷之间的作用力只能与距离平方成反比。虽然这个思想很重要，但是普利斯特利的结论在当时并没有得到科学界的重视。

在库仑定律提出前有两个人曾作过定量的实验研究，并得到明确的结论。可惜，都没有及时发表而未对科学的发展起到应有的推动作用。一位是英国爱丁堡大学的罗宾逊，认为电力服从平方反比律，并且得到指数n=2.06，从而电学的研究也就开始进行精确研究。不过，他的这项工作直到1801年才发表。另一位是英国的卡文迪许。1772～1773年间，他做了双层同心球实验，第一次精确测量出电作用力与距离的关系。发现带电导体的电荷全部分布在表面而内部不带电。卡文迪许进一步分析，得到n=20.02。他的这个同心球实验结果在当时的条件下是相当精确的。但可惜的是他一直没有公开发表这一结果。

定律建立

库仑是法国工程师和物理学家。1785年，库仑用扭称实验测量两电荷之间的作用力与两电荷之间距离的关系。他通过实验得出：“两个带有同种类型电荷的小球之间的排斥力与这两球中心之间的距离平方成反比。”同年，他在《电力定律》的论文中介绍了他的实验装置，测试经过和实验结果。

库仑的扭秤巧妙的利用了对称性原理按实验的需要对电量进行了改变。库仑让这个可移动球和固定的球带上同量的同种电荷，并改变它们之间的距离。通过实验数据可知，斥力的大小与距离的平方成反比。但是对于异种电荷之间的引力，用扭称来测量就碰到了麻烦。经过反复的思考，库仑借鉴动力学实验加以解决。库仑设想：假如异种电荷之间的引力也是与它们之间的距离平方成反比，那么只要设计出一种电摆就可进行实验。

通过电摆实验，库仑认为：“异性电流体之间的作用力，与同性电流体的相互作用一样，都与距离的平方成反比。”库仑利用与单摆相类似的方法测定了异种电荷之间的引力也与它们的距离的平方成反比，不是通过扭力与静电力的平衡得到的。可见库仑在确定电荷之间相互作用力与距离的关系时使用了两种方法，对于同性电荷，使用的是静电力学的方法；对于异性电荷使用的是动力学的方法。

库仑注重修正实验中的误差，最后得到：“在进行刚才我所说的必要的修正后，我总是发现磁流体的作用不管是吸引还是排斥都是按距离平方倒数规律变化的。”但是应当指出的是，库仑只是精确的测定了距离平方的反比关系，并把静电力和静磁力从形式归纳于万有引力的范畴，我们这里要强调的是库仑并没有验证静电力与电量之积成正比。“库仑仅仅认为应该是这样。也就是说库仑验证了电力与距离平方成反比，但仅仅是推测电力与电量的乘积成正比。”

验证影响

库仑定律是平方反比定律，自发现以来，科学家不断检验指数2的精度。1971年威廉等人的实验表明库仑定律中指数2的偏差不超过10^-16，因此假定为2。事实上，指数为2和光子静止质量为零是可以互推的。其实假如mz不为零，即使这个值很小，也会动摇物理学大厦的重要基石，因为现有理论都是以mz等于零为前提。到目前为止，理论和实验表明点电荷作用力的平方反比定律是相当精确的。200多年来，电力平方反比律的精度提高了十几个数量级，使它成为当今物理学中最精确的实验定律之一。回顾库仑定律的建立过程，库仑并不是第一个做这类实验的人，而且他的实验结果也不是最精确的。我们之所以把平方反比定律称为库仑定律是因为库仑结束了电学发展的第一个时期。库仑的工作使静电学趋于高度完善。电量的单位也是为了纪念库仑而以他的名字命名的。

库仑定律不仅是电磁学的基本定律，也是物理学的基本定律之一。库仑定律阐明了带电体相互作用的规律，决定了静电场的性质，也为整个电磁学奠定了基础。库仑从1777年起就致力于把超距作用引入磁学和电学。他认为静电力和静磁力都来自远处的带电体和荷磁体，并不存在什么电流体和涡旋流体对带电物质和磁体的冲击；这些力都符合牛顿的万有引力定律所确定的关系。库仑提供了精密的测量，排除了关于电本性的一切思辩。库仑的工作对法国物理学家的影响还可以从稍后的拉普拉斯的物理学简略纲领得到证实。这个物理学简略纲领最基本的出发点是把一切物理现象都简化为粒子间吸引力和排斥力的现象，电或磁的运动是荷电粒子或荷磁粒子之间的吸引力和排斥力产生的效应。这种简化便于把分析数学的方法运用于物理学。

过程地位

1767年，英格兰化学家约瑟夫・普利斯特里猜测电荷之间的相互作用力具有类似于万有引力的的平方反比形式。

1769年，苏格兰物理学家约翰・罗比逊首次通过实验发现两个带电球体之间的作用力与它们之间距离的2.06次方成反比。

1770年代早期，著名英国物理学家亨利・卡文迪什通过巧妙的实验，得出了带电体之间的作用力依赖于带电量与距离，并得出静电力与距离的 成反比，只是卡文迪什没有公布这个结果。

后来，麦克斯韦利用与卡文迪什类似的方法，得出静电力与距离的 成反比的结果。

库仑定律是电学的基本定律，其中平方反比关系是否精确成立尤其重要，而根据现代量子场论，静电力的平方反比关系是与光子的静质量是否精确为零相关的，所以，对静电力的平方反比关系的精确验证，关系着现代物理学基本理论的基础。当前对库仑定律平方反比关系的验证越来越精确，如1971年进行的一次实验，给出库仑定律与平方反比关系的偏差小于。

库仑定律_库仑定律 -注意事项

(1) 库仑定律只适用于计算两个点电荷间的相互作用力，非点电荷间的相互作用力,库仑定律不适用。（不能根据直接认为当r无限小时F就无限大，因为当r无限小时两电荷已经失去了作为点电荷的前提。）

(2) 应用库仑定律求点电荷间相互作用力时，不用把表示正,负电荷的"+","-"符号代入公式中计算过程中可用绝对值计算，其结果可根据电荷的正,负确定作用力为引力或斥力以及作用力的方向。

(3)库仑力一样遵守牛顿第三定律，不要认为电荷量大的对电荷量小的电荷作用力大。(两电荷之间是作用力和反作用力) 。

库仑定律_库仑定律 -典型例题

爱华网本文地址 » http://www.aihuau.com/a/8104090103/174491.html