发布时间:2018年04月10日 22:15:42分享人:桃色周刊来源:互联网13
所谓二进制,就是用0和1两个数码来表示的数。二进制是计算技术中广泛采用的一种数制。二进制的基数为2,二进制进位规则是“逢二进一”,二进制借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统。二进制的或运算:遇1得1,二进制的与运算:遇0得0,二进制的非运算:各位取反。
二进制算法_二进制算法 -法则
各位取反加法法则:0+0=0,0+1=1+0=1,1+1=10
减法,当需要向上一位借数时,必须把上一位的1看成下一位的(2)10。
减法法则:0-0=0,1-0=1,1-1=0,0-1=1有借位,借1当(10)看成2则0-1-1=0有借位1-1-1=1有借位。
乘法法则:0×0=0,0×1=0,1×0=0,1×1=1
除法应注意:0÷0=0(无意义),0÷1=0,1÷0=0(无意义)
除法法则:0÷1=0,1÷1=1
二进制算法_二进制算法 -格式

二进制与十进制的算法格式相同,只不过十进制是逢十进一,而二进制是逢二进一。
爱华网本文地址 » http://www.aihuau.com/a/8104090103/175321.html
更多阅读
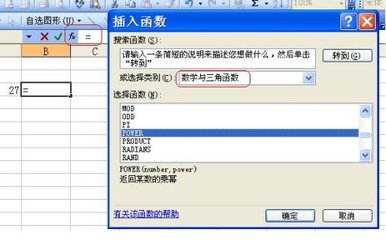
【问题】EXCEL如何进行开方运算?【解答】例如将27开5次方,可以在单元格中输入 =27^(1/5) 。如下图:
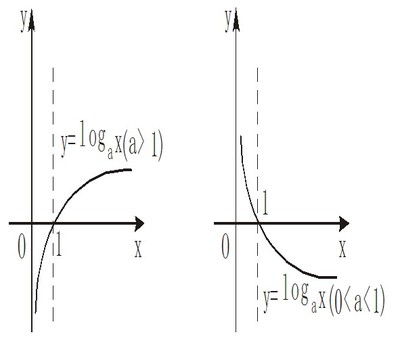
一、教材分析本小节主要内容是学习对数函数的定义、图象、性质及初步应用。对数函数是继指数函数之后的又一个重要初等函数,无论从知识或思想方法的角度对数函数与指数函数都有许多类似之处。与指数函数相比,对数函数所涉及的知识更
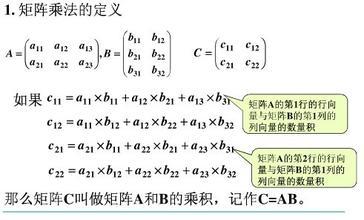
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////#include#define SIZE 20 //预定义要进行转置的矩阵最大大小为 20*20//为了函

模指数运算:exp(a,e)modm。最后都转化为一系列的模乘法运算。提高模指数运算速度的有效方法是减少模指数运算中模乘法耳朵次数。以二进制算法为例:设e=(e0 e1 e2 ...)2,即将e转化为二进制序列;1 初始化,t=exp(a,e0);2 遍历e的二进制序列

现有的有负数的加减乘除法的运算法则的推导方法从效果上说主要存在以下两个缺陷:1、没有简单的独立的减法运算法则(当然复杂的就不会让它出笼).2、没有求多个整数的连加式的和由计算法变为接龙看数法.现有推导方法犯了逻辑错误,具体说主

 爱华网
爱华网



