十字相乘法能把某些二次三项式分解因式。要务必注意各项系数的符号。十字相乘法能把某些二次三项式分解因式。对于形如ax2+bx+c=(a1x+c1)(a2x+c2)的整式来说,方法的关键是把二次项系数a分解成两个因数a1,a2的积a1・a2,把常数项c分解成两个因数c1,c2的积c1・c2,并使a1c2+a2c1正好是一次项的系数b,那么可以直接写成结果:ax2+bx+c=(a1x+c1)(a2x+c2)。在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,往往需要多次试验,务必注意各项系数的符号。基本式子:x2+(p+q)x+pq=(x+p)(x+q)。
十字相乘法_十字相乘法 -概念
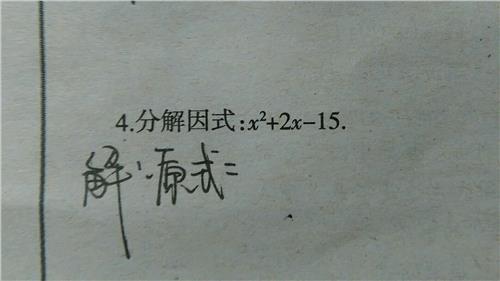
十字相乘法的方法
十字相乘法简单来讲就是:十字左边相乘等于二次项,右边相乘等于常数项,交叉相乘再相加等于一次项。其实就是运用乘法公式(x+a)(x+b)=x2+(a+b)x+ab的逆运算来进行因式分解。
十字相乘法能把某些二次三项式分解因式。对于形如ax2+bx+c=(a1x+c1)(a2x+c2)的整式来说,方法的关键是把二次项系数a分解成两个因数a1,a2的积a1・a2,把常数项c分解成两个因数c1,c2的积c1・c2,并使a1c2+a2c1正好是一次项的系数b,那么可以直接写成结果:ax2+bx+c=(a1x+c1)(a2x+c2)。在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,往往需要多次试验,务必注意各项系数的符号。基本式子:x2+(p+q)x+pq=(x+p)(x+q)。
十字相乘法_十字相乘法 -通俗方法
十字相乘法例:
a2x2+ax-42
首先,我们看看第一个数,是a2,代表是两个a相乘得到的,则推断出(a×+?)×(a×+?),
然后我们再看第二项,+a这种式子是经过合并同类项以后得到的结果,所以推断出是两项式×两项式。
再看最后一项是-42,-42是-6×7或者6×-7也可以分解成-21×2或者21×-2。
首先,21和2无论正负,通过任意加减后都不可能是1,只可能是-19或者19,所以排除后者。
然后,再确定是-7×6还是7×-6。
(a×-7)×(a×+6)=a2x2-ax-42(计算过程省略)
得到结果与原来结果不相符,原式+a变成了-a。
再算:
(a×+7)×(a×+(-6))=a2x2+ax-42
正确,所以a2x2+ax-42就被分解成为(ax+7)×(ax-6),这就是通俗的十字相乘法分解因式。
十字相乘法_十字相乘法 -例题解析
例1
把2x2-7x+3分解因式。
分析:先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分
别写在十字交叉线的右上角和右下角,然后交叉相乘,求代数和,使其等于一次项系数。
分解二次项系数(只取正因数因为取负因数的结果与正因数结果相同!)。
2=1×2=2×1;
分解常数项:
3=1×3=3×1=(-3)×(-1)=(-1)×(-3).
用画十字交叉线方法表示下列四种情况:
13
 爱华网
爱华网