罗尔中值定理是微分学中一条重要的定理,是三大微分中值定理之一,描述如下: 如果函数f(x)满足以下条件:(1)在闭区间[a,b]上连续,(2)在(a,b)内可导,(3)f(a)=f(b),则至少存在一个ξ∈(a,b),使得f'(ξ)=0。
罗尔中值定理_罗尔中值定理 -证明过程
证明:因为函数f(x)在闭区间[a,b]上连续,所以存在最大值与最小值,分别用M和m表示,分两种情况讨论:
1. 若M=m,则函数f(x)在闭区间[a,b]上必为常数,结论显然成立。
2. 若M>m,则因为f(a)=f(b)使得最大值M与最小值m至少有一个在(a,b)内某点ξ处取得,从而ξ是f(x)的极值费马引理点,由条件f(x)在开区间(a,b)内可导得f(x)在ξ处可导,故由推知:f'(ξ)=0。
罗尔中值定理_罗尔中值定理 -罗尔中值定理的几何意义
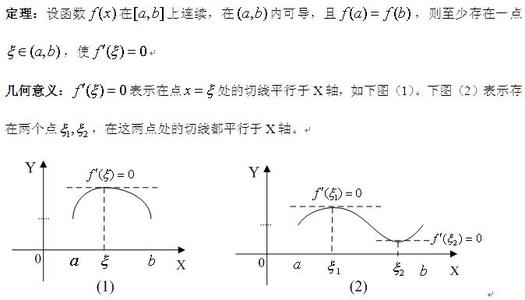
若连续曲线y=f(x)在区间[a,b]上所对应的弧段AB,除端点外处处具有不垂直于x轴的切线,且在弧的两个端点A,B处的纵坐标相等,则在弧AB上至少有一点C,使曲线在C点处的切线平行于x轴。
罗尔中值定理_罗尔中值定理 -范例解析
罗尔中值定理
用罗尔中值定理证明:方程
在(0,1)内有实根。
罗尔中值定理
设
,则F(x)在[0,1]上连续,在(0,1)内可导,
,所以由罗尔中值定理,至少存在一点
,使得
,所以
,所以ξ是方程方程
在(0,1)内的一个实根。
结论得证。
 爱华网
爱华网