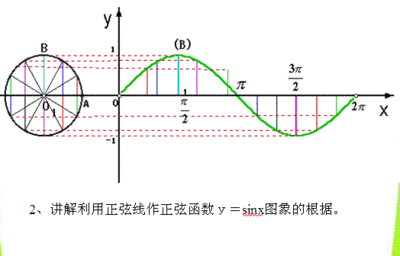
正弦函数是数学领域的一个定义。正弦函数是三角函数的一种,在直角三角形ABC中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正弦函数就是sinA=a/c,即sinA=BC/AB。定义:对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sin x,这样,对于任意一个实数x都有唯一确定的值sin x与它对应,按照这个对应法则所建立的函数,表示为f(x)=sin x,叫做正弦函数。正弦函数的定理:在一个三角形中,各边和它所对角的正弦的比相等,即a/sin A=b/sin B=c/sin C。
正弦函数_正弦函数 -简介
正弦函数当正弦函数的形式为:y=Asin(ωx+φ)时。这里只讨论A大于零的情况。该函数的定义域为R。值域:【-A,A】。
最值:(1)最大值:当x=(π/2+2kπ-φ)/ω时,y(max)=A。
(2)最小值:当x=(-(π/2)+2kπ-φ)/ω时,y(min)=-A。
零值点:((kπ-φ)/ω,0)
对称性:(1)对称轴:关于直线x=(π/2)+kπ对称.
(2)中心对称:关于点((kπ-φ)/ω,0)对称。
周期:(2π-φ)/ω。
奇偶性:奇函数。
单调性:在【(-(π/2)+2kπ-φ)/ω,(π/2+2kπ-φ)/ω】上是增函数;
在【(π/2+2kπ-φ)/ω,(3π/2+2kπ-φ)/ω】上是减函数。
正弦函数_正弦函数 -定义
三角函数的一种。
在直角三角形ABC中,角C等于90度,AB是斜边,BC是角A的对边,AC是角A的邻边
正弦函数就是sin(A)=a/h
正弦函数_正弦函数 -性质
解析式:y=sinx
图象:波形图象
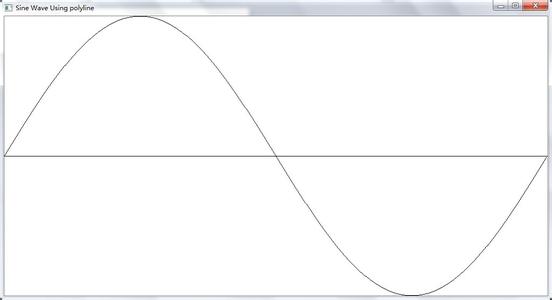
定义域:R
值域:【-1,1】
最值:
①最大值:当x=(π/2)+2kπ时,y(max)=1
②最小值:当x=-(π/2)+2kπ时,y(min)=-1
零值点:
(kπ,0)
对称性:
1)对称轴:关于直线x=(π/2)+kπ对称
2)中心对称:关于点(kπ,0)对称
周期:2π
奇偶性:奇函数
单调性:在【-(π/2)+2kπ,(π/2)+2kπ】上是增函数,在【(π/2)+2kπ,(3π/2)+2kπ】上是减函数
正弦函数_正弦函数 -函数性质
正弦型函数解析式:y=Asin(ωx+φ)+h
各常数值对函数图像的影响:
φ(初相位):决定波形与X轴位置关系或横向移动距离(左加右减)
ω:决定周期(最小正周期T=2π/|ω|)
A:决定峰值(即纵向拉伸压缩的倍数)
h:表示波形在Y轴的位置关系或纵向移动距离(上加下减)
作图方法运用“五点法”作图
“五点作图法”即当ωx+φ分别取0,π/2,π,3π/2,2π时y的值.
单位圆定义
图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。这个交点的y坐标等于sinθ。在这个图形中的三角形确保了这个公式;半径等于斜边并有长度1,所以有了sinθ=y/1。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于1查看无限数目的三角形的一种方式。即sinθ=AB,与y轴正方向一样时正,否则为负
对于大于2π或小于0的角度,简单的继续绕单位圆旋转。在这种方式下,正弦变成了周期为2π的周期函数。
 爱华网
爱华网