拉姆齐二染色定理,这个定理以弗兰克・普伦普顿・拉姆齐命名,在组合数学上,拉姆齐(Ramsey)定理是要解决以下的问题:要找这样一个最小的数n,使得n个人中必定有k个人相识或l个人互不相识。
拉姆齐二染色定理_拉姆齐二染色定理 -来源
拉姆齐二染色定理以弗兰克・普伦普顿・拉姆齐命名,1930年他在论文OnaProbleminFormalLogic(《形式逻辑上的一个问题》)证明了R(3,3)=6。
拉姆齐二染色定理_拉姆齐二染色定理 -相关概念
拉姆齐二染色定理
拉姆齐数的定义
拉姆齐数,用图论的语言有两种描述:对于所有的N顶图,包含k个顶的团或l个顶的独立集。具有这样性质的最小自然数N就称为一个拉姆齐数,记作R(k,l);在着色理论中是这样描述的:对于完全图Kn的任意一个2边着色(e1,e2),使得Kn[e1]中含有一个k阶子完全图,Kn[e2]含有一个l阶子完全图,则称满足这个条件的最小的n为一个拉姆齐数。(注意:Ki按照图论的记法表示i阶完全图)拉姆齐证明,对与给定的正整数数k及l,R(k,l)的答案是唯一和有限的。
拉姆齐数亦可推广到多于两个数
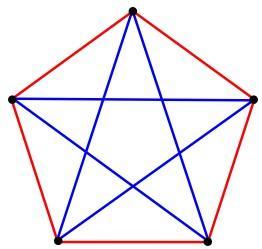
对于完全图Kn的每条边都任意涂上r种颜色之一,分别记为e1,e2,e3,...,er,在Kn中,必定有个颜色为e1的l1阶子完全图,或有个颜色为e2的l2阶子完全图……或有个颜色为er的lr阶子完全图。符合条件又最少的数n则记为R(l1,l2,l3,...,lr;r)。
拉姆齐数的数值或上下界
已知的拉姆齐数非常少,保罗・艾狄胥曾以一个故事来描述寻找拉姆齐数的难度:“想像有队外星人军队在地球降落,要求取得R(5,5)的值,否则便会毁灭地球。在这个情况,我们应该集中所有电脑和数学家尝试去找这个数值。若它们要求的是R(6,6)的值,我们要尝试毁灭这班外星人了。”
r,s345678910369141823283640
 爱华网
爱华网