纳什均衡点(港译:纳殊均衡点),又称为非合作博弈均衡点,是博弈论的一个重要概念,以约翰・纳什命名。
纳什均衡点(Nash Equilibrium Point)
纳什均衡点_纳什均衡点 -纳什均衡点概述
纳什均衡点(港译:纳殊均衡点),又称为非合作博弈均衡点,是博弈论的一个重要概念,以约翰・纳什命名。
如果某情况下无一参与者可以独自行动而增加收益,则此策略组合被称为纳什均衡点。
纳什均衡点概念提供了一种非常重要的分析手段,使博弈论研究可以在一个博弈结构里寻找比较有意义的结果。
但纳什均衡点定义只局限于任何局中人不想单方面变换策略,而忽视了其他局中人改变策略的可能性,因此,在很多情况下,纳什均衡点的结论缺乏说服力,研究者们形象地称之为“天真可爱的纳什均衡点”。
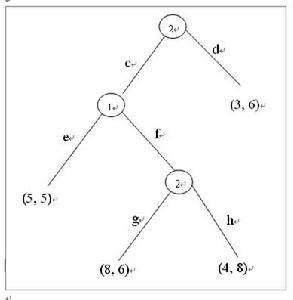
纳什均衡点_纳什均衡点 -什么是纳什均衡点呢?
简单说就是,一策略组合中,所有的参与者面临这样的一种情况,当其他人不改变策略时,他此时的策略是最好的,也就是说,此时如果他改变策略,他的支付将会降低,在纳什均衡点上,每一个理性的参与者都不会有单独改变策略的冲动。
有些博弈的纳什均衡点不止一个。如下述“夫妻博弈”(或称性别之战)中有两个纳什均衡点。丈夫和妻子商量晚上的活动。丈夫喜欢看拳击,而妻子喜欢欣赏歌剧。但两人都希望在一些度过夜晚。在这个“夫妻博弈”中有两个纳什均衡点:(歌剧,歌剧),(拳击,拳击)在有两个或两个以上纳什均衡点的博弈中,其最后结果难以预测,在“夫妻博弈”中,我们无法知道,最后结果是一同欣赏歌剧还是一起去看拳击。
启示:通俗地说,纳什均衡含义就是:给定你的策略,我的策略是最好的策略;给定我的策略,你的策略也是你最好的策略,即双方在对方给定的策略下不愿意调整自己的策略。
纳什均衡点_纳什均衡点 -纳什均衡有什么用
纳什的想法成为我们指导同时行动博弈的最后一个法则的基础,这个法则如下:走完寻找优势策略剔除劣势策略的捷径之后,下一步就是寻找这个博弈的均衡。
我们还要解释一下这个法则,为什么一个博弈的参与者非得达到这么一个结局呢?我们可以说出好几个理由。没有一个理由本身就有足够的说服力,不过,只要把几个理由结合起来,变能形成一个有力的答案。
首先,存在避免循环推理的必要,因为循环推理帮不上忙。均衡在没完没了的“我知道他知道我知道-----”的循环里是稳定不变的,这使参与者对其他人的行动的估计能保持连贯性。各方正确预计别人的行动,并且确定自己的最佳对策。
均衡策略的第二个好处出现在零和博弈中。在这种博弈里,参与者的利益严格相悖。你的对手不能通过引诱你采取一个均衡策略而得到任何好处。你已经充分考虑到他们对你正在做的事情会有什么样的最佳对策。
第三个理由是,均衡方法注重实效。要想知道梨子的滋味,就要吃一吃。我们将会利均衡方法讨论许多博弈。希望读教师为检验它对博弈结果的预测以及这种思维方式产生的行为指导方针,相信这么做会使我们的分析有意思,比抽象地讨论均衡方法的优点更有意义。
最后,可能存在一个对均衡概念的误解,希望各位可以避免。当我们说博弈的结果是均衡,并不一下是对参与者最有利的结果,更不意味着是对整个社会作为一个整体而言最有利的结果。有利或者不利的评价永远属于另外一个问题,答案视各个案例的具体情况而各有不同。
在经济学中,均衡意即相关量处于稳定值。在供求关系中,某一商品市场如果在某一价格下,想以此价格买此商品的人均能买到,而想卖的人均能将商品卖出去,此时我们就说,该商品的供求达到了均衡。此时的价格可称之为均衡价格,产量称之为均衡产量。均衡分析是经济学中的经要分析。
那么什么是博弈论的均衡呢?所谓博弈均衡,它是一稳定的博弈结果。均衡是博弈的一结果,但不是说博弈的结果都能成为均衡。博弈的均衡是稳定的,因而是可以预测的。
纳什均衡是一最常见的均衡。它的含义是:在对方策略确定的情况下,每个参与者的策略都是最好的,此时没有人愿意先改变自己的策略。
在上面的“买----卖”的博弈中,可以解释为什么在现实中讨价还价后买卖能做成的原因,因为这对双方来说都有是最优选择。同时在“买-----卖”博弈中,其均衡对双方来说是全局最优的。
纳什均衡点_纳什均衡点 -经典的例子
经典的例子就是囚徒困境,囚徒困境是一个非零和博弈。大意是:一个案子的两个嫌疑犯被分开审讯,警官分别告诉两个囚犯,如果你招供,而对方不招供,则你将被判刑一年,而对方将被判刑十年;如果两人均招供,将均被判刑五年。 于是,两人同时陷入招供还是不招供的两难处境。如果两人均不招供,将最有利,只被判刑三年。但两人无法沟通,于是从各自的利益角度出发,都依据各自的理性而选择了招供, 这种情况就称为纳氏均衡点。这时,个体的理性利益选择是与整体的理性利益
Image:博弈论-囚徒困境.jpg
基于经济学中Rational agent的前提假设,两个囚犯符合自己利益的选择是坦白招供,原本对双方都有利的策略不招供从而均被判刑三年就不会出现。事实上,这样两人都选择坦白的策略以及因此被判五年的结局被是“纳什均衡”(也叫非合作均衡),换言之,在此情况下,无一参与者可以“独自行动”(即单方面改变决定)而增加收获。
纳什均衡点_纳什均衡点 -学术争议和批评
(供参考)
第一,纳什(Nash)的关于非合作(non-cooperative)博弈论的平衡不动点解(equilibrium/fixpoint)学术证明是非构造性的(non-constructive),就是说纳什用角谷静夫不动点定理(Kakutani fixed point theorem)证明了平衡不动点解是存在的,但却不能指出以什么构造算法如何去达到这个平衡不动点解。这种非构造性的发现对现实生活里的博弈的作用是有限的,即使知道平衡不动点解存在,在很多情况下达不到并不能解决问题。来源请求在数学意义上,纳什并没有超越角谷静夫不动点定理。
经过《美丽心灵》的Sylvia Nasar(书作者)和Ron Howard(电影作者)这样的主流媒体的介入,角谷静夫(Kakutani)在这些人的作品里被完全忽略。有人认为,“纳什平衡”(Nash equilibrium)的更合适的名字应该叫作“角谷静夫―纳什博弈论不动点”(Kakutani-Nash game-theoretic fixed point)或“角谷静夫―纳什平衡”(Kakutani-Nash equilibrium),没有角谷静夫不动点定理,纳什的证明没有多大学术意义。《美丽心灵》完全忽视角谷静夫之关键贡献的作法有待商榷。 第二,纳什的非合作(non-cooperative)博弈论模型仅仅是突破了博弈论中的一个局限。一个更大的局限是,博弈论面对的往往是由几十亿节点的庞大对象构成的社会、经济等复杂行为,但冯・诺伊曼(Von Neumann)和纳什的研究是针对两三个节点的小规模博弈论(有人称之为tiny-scale toy case)。
这个假设的不完善处,可能比假设大家都是合作的(cooperative)更严重。因为在经济学里,一个庞大社会里的人极不可能全部都是合作的,非合作的情况通常在庞大对象的情形中更普遍,而在两三个节点的小规模经济中倒反而影响较小。既然改了合作前提为非合作前提,却仍然停留在两三个节点的小规模博弈论中,这是一个不可忽视的缺陷。最近香港城市大学和北京清华大学的学者群邓小铁、姚期智在基于复杂度理论的大规模博弈论上有所进展,这和纳什小规模博弈论的本质以及《美丽心灵》的广告效果是不可同日而语的。
 爱华网
爱华网