如何找出随机数的规律 找出规律，数列前n项和的公式就再不会记错了

中学数学课学习的数列知识，需要我们牢记好多公式。

常用有这么多数列，如果规律不明显，前n项和公式记起来就麻烦了，怎么样才能轻松记牢呢？

别着急，我找到规律，大家一起看看吧

1+ 2+ 3+ 4 +……+ n = n(n+1)/2

2+ 4+ 6+ 8 +……+ 2n = n(n+1)

1+ 3+ 5+ 7 +……+ 2n-1 = n"

等差数列，规律明显，我们都用不着记

1+ 4+ 9+ 16 +……+ n"

1"+ 3"+ 5"+ 7" +……+ (2n-1)"

1+ 8+ 27+ 64 +……+ n^3

1 + 27 + 125 +……+ (2n-1)^3

数列通项有二次方、完全平方式，还有三次方，前n项和公式记得方便吗？

1+ 3+ 6+ 10 +……+ n(n+1)/2

1X2 + 2X3 + 3X4 + 4X5 +……+ n(n+1)

1X2X3 + 2X3X4 + 3X4X5 + 4X5X6 +……+ n(n+1)(n+2)

数列通项是连续数字的乘积，前n项和又是什么呢？

1/2 + 1/6 + 1/12 + 1/20 +……+ 1/n(n+1)

1/6+ 1/24 + 1/60 + 1/120 +……+ 1/n(n+1)(n+2)

数列通项变成连续数字乘积的倒数，找规律算前n项和，是不是更困难了呢？

为什么自然数列 1、2、3、4……通项为 n，前n项和就是 n(n+1)/2 呢？

找规律，让我们抛开等差数列，换个思路看看

1 = 1 X (1+1) / 2 = 1 X 2 / 2

1+ 2 = 3 = 2 X (2+1) / 2 = 2 X 3 / 2

1+ 2+ 3 = 6 = 3 X (3+1) / 2 = 3 X 4 / 2

1+ 2+ 3+ 4 = 10 = 4 X (4+1) / 2 = 4 X 5 / 2

看到 1X2 /2、2X3 /2、3X4 /2、4X5 /2，你有没有得到启发呢？

我就觉得，这个 n(n+1)/2，并非梯形面积 (a+b) h / 2 那样，最大项加最小项的和，乘以项数以后，去掉重复除以2；

这个 n(n+1)/2，或许正是为了变成连续数字的乘积。

让我们取自然数列的前三项，看看吧

1+ 2+ 3

= 2 X (1+2+3) / 2

= [ 1X2 + 2X2 + 3X2 ] / 2

= [ 1X2 + 2X(3-1) + 3X(4-2) ] / 2

= [ 1X2 -1X2 +2X3 -2X3 +3X4 ] / 2

= 3 X 4 / 2

= 3 X (3+1) / 2

这个自然数列，第一项是 1 ，变成连续数字的乘积就是 1X2 ，计算前 n 项的和，就要把整个数列乘以 2 和倒数 1/2 ，确保和不变；然后就可以把 2 变成不同两个数字的差，各个数项与它们相乘之后，变成一组组连续数字的乘积，前面各项相互抵消，最后就只剩下最大项变的 n(n+1)/2

是这样吗？通项是连续两个数字乘积的数列，也取前三项试试看

1X2 + 2X3 + 3X4

= 3 X ( 1X2 + 2X3 + 3X4 ) / 3

= [ 1X2X3 + 2X3X(4-1) + 3X4X(5-2) ] / 3

= [ 1X2X3 - 1X2X3 + 2X3X4 - 2X3X4 + 3X4X5 ] / 3

= 3 X 4 X 5 / 3

= 3 X (3+1) X (3+2) / 3

没错，这个数列 2、6、12、20……通项 n(n+1)，第一项是 1X2，计算前n项和就要变成 1X2X3，整个数列就要乘以 3 和 1/3，各个数项乘以 3 之后，就变成一组组相互抵消的连续数字乘积，最后只剩下最大项变的 n(n+1)(n+2)/3

显然，换成数列 1、3、6、10……通项为 n(n+1)/2，前n项和就是 n(n+1)(n+2)/6

接下来，我们继续看看，通项是连续三个数字乘积的数列

1X2X3 + 2X3X4 + 3X4X5

= [ 1X2X3X4 + 2X3X4X(5-1) + 3X4X5X(6-2) ] / 4

= [ 1X2X3X4 - 1X2X3X4 + 2X3X4X5 - 2X3X4X5 + 3X4X5X6 ] / 4

= 3 X 4 X 5 X 6 / 4

= 3 X (3+1) X (3+2) X (3+3) / 4

同理，这个数列的通项是 n(n+1)(n+2)，前n项和就是 n(n+1)(n+2)(n+3)/4

看到这里，这个规律我们就更清楚了。

数列 1、2、3、4……通项是 n，前n项和就是 n(n+1)/2；

数列 2、6、12、20……通项是 n(n+1)，前n项和就是 n(n+1)(n+2)/3

数列 6、24、60、120……通项是 n(n+1)(n+2)，前n项和就是 n(n+1)(n+2)(n+3)/4

还有通项是连续数字乘积倒数的数列，肯定也是大同小异吧

1/(1X2) + 1/(2X3) + 1/(3X4)

= (2-1)/(1X2) + (3-2)/(2X3) + (4-3)/(3X4)

= 1 -1/2 + 1/2 -1/3 + 1/3 -1/4

= 1 -1/4

= 3/4

连续三个数字乘积的倒数

1/(1X2X3) + 1/(2X3X4) + 1/(3X4X5)

= (1/2) X [ (3-1)/(1X2X3) + (4-2)/(2X3X4) + (5-3)/(3X4X5) ]

= (1/2) X [ 1/(1X2) -1/(2X3) + 1/(2X3) -1/(3X4) + 1/(3X4) -1/(4X5) ]

= (1/2)[ 1/(1X2) -1/(4X5) ]

哦！难怪如此

数列 1/2、1/6、1/12 ……通项是 1/n(n+1)，

前n项和就是 n/(n+1)；

数列 1/6、1/24、1/60 ……通项是 1/n(n+1)(n+2)，

前n项和就是 (1/2)[ 1/(1X2) - 1/(n+1)(n+2) ]

自然数二次方，1、4、9、16、25……通项是 n" 这个数列

显然，1X2= 1"+1，2X3= 2"+2，n(n+1)= n"+n，我们就正好用那两个数列前n项和的公式相减，算出这个通项为 n" 的数列前n项和

n(n+1)(n+2)/3 - n(n+1)/2

= n(n+1)[2(n+2)/6 - 3/6]

= n(n+1)[2n+4-3]/6

= n(n+1)(2n+1)/6

数列的通项是 n"，前n项和就是 n(n+1)(2n+1)/6

奇数的二次方 1、9、25、49、81……通项是 (2n-1)" 这个数列

还是先取前三项看看

1X1 + 3X3 + 5X5

= 1 + 3X(1+2) + 5X(2+3)

= [ 1X2 + 3X(2+4) + 5X(4+6) ] / 2

= [ 1X2 + 2X3 + 3X4 + 4X5 + 5X6 ] / 2

= 5 X 6 X 7 / 6

这样就再次看到了，连续数字乘积的形式

= 2n (2n - 1) (2n + 1) / 6

= n (4n" - 1) / 3

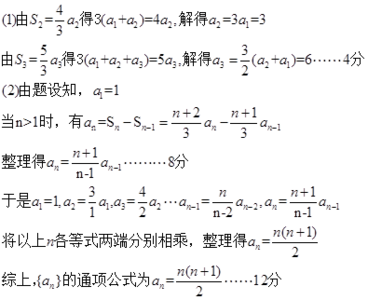
数列的通项是 (2n-1)"，前n项和就是 2n(2n+1)(2n-1)/6 = n(4n"-1)/3

看到了吗？通项是二次方的数列，前n项和的式子中都有因式 n(2n+1)，记住他们这个共同特征，数列前n项和的公式，我们就不会记错了。

自然数三次方 1、8、27、64、125……通项是 n^3 这个数列

我们也用连续数字的乘积来试试，

要知道，一个数的三次方，变成连续数字的乘积就更方便了，看吧

5 X 5 X 5

= 5X( 5" - 1" + 1)

= 5X(5 - 1)(5 + 1) + 5 X 1

= 4X5X6 + 5

数列我们就取前四项看看吧

1X1X1 + 2X2X2 + 3X3X3 + 4X4X4

= 1+ 2+ 3+ 4+ 1X2X3 + 2X3X4 + 3X4X5

= 4X5 /2 + [ 1X2X3X4 + 2X3X4X(5-1) + 3X4X5X(6-2) ] / 4

= 4X5X2 /4 + 3X4X5X6 /4

= 4X5 X ( 2 + 3X6 ) / 4

= 4X5 X ( 2 + 2X9 ) / 4

= 4X5 X (2X10) / 4

= (4X5/2)"

= [ 4 X ( 4 + 1 ) / 2 ]"

数列的通项是 n^3，前n项和就是 [n(n+1)/2]"

其实

1 + 8 + 27 + 64 + 125

= 9 + 27 + 64 + 125

= 36 + 64 + 125

= 100 + 125

= 225

这个数列只要把前几项像这样耐心地加一遍，我们就会发现，1、9、36、100、225这几个前n项的和，也正好是 1、3、6、10、15……n(n+1)/2 的二次方。

奇数的三次方 1、27、125……通项是 (2n-1)^3 这个数列

我们还是变成连续数字的乘积，取前四项看看

1X1X1 + 3X3X3 + 5X5X5 + 7X7X7

= 1+ 3+ 5+ 7 + 2X3X4 + 4X5X6 + 6X7X8

= 4X4 + 2X1X3X2X2 + 2X2X5X3X2 + 2X3X7X4X2

= 4X4 + 4X1X2X3 + 4X2X3X5 + 4X3X4X(5+2)

= 4X4 + 1X2X3X4 + 2X3X4X5 + 2X3X4X4 + 3X4X5X4

= 4X4 + 1X2X3X4 + 2X3X4X(5-1) + 2X3X4X5 + 3X4X5X(6-2)

= 4X4 + 2X3X4X5 + 3X4X5X6

= 4X4 + 3X4X5X8

= n" + [ 2n (n-1) n (n+1) ]

= n" + [ 2n"(n" - 1) ]

= n" + 2(n^4) - 2n"

= 2(n^4) - n"

= n"(2n" - 1)

数列的通项是 (2n-1)^3，前n项和就是 n"(2n"-1)

经过一番探索，这些数列的前n项和公式，我们都自己推导出来，找出规律了，印象一定也加深了不少。假如我们今后一时想不起公式，就可以根据这个规律，自己重新把公式推导出来。如今我们也得到了思路，知道公式是怎么得来的，这样也再不会记错了。

通项是连续数字乘积的数列，前n项和都是把最后一项变形，继续乘以下一个数字，最后一项总共变成多少数字相乘，最终就要除以多少。

正如 1X2X3 + 2X3X4 + 3X4X5 +……+ n(n+1)(n+2)= n(n+1)(n+2)(n+3)/4，数列通项是 n(n+1)(n+2)，前n项和就把通项乘以(n+3)，然后除以4

利用连续数字的乘积，变形得到数列通项的最高次项，然后把多项式变得等于原来的通项式，就可以利用已知的数列公式，组合算出这个数列的前n项和公式了。

这种通项是连续数字乘积的数列，帮助我们把这些幂函数的数列公式都记住了。我们学习知识就要多多开动脑筋，积极探索，总结经验，把一个个知识点挂钩串联起来，得到一条思路，这样才学得牢固。

一个个知识点也正如一个个果实，肯定要“顺藤摸瓜”才回忆得方便轻松；假如一个个知识点在脑子里面“一盘散沙”，我们需要时找不到，想不起来，这样和不知道又有什么差别呢？

爱华网本文地址 » http://www.aihuau.com/a/8104150103/192889.html