反思一:勾股定理的逆定理教学反思
一、本节课的成功之处:
本节课以活动为主线,通过从估算到实验活动结果的产生让学生总结过程,最后回到解决生活中实际问题,思路清晰,脉络明了。
例如:活动1问题:据说古埃及人用下图的方法画直角:把一根长蝇打上等距离的13个结,然后以3个结,4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
这个问题意味着,如果围成的三角形的三边分别为3、4、5.有下面的关系“32+42=52”.那么围成的三角形是直角三角形.
2、体现了“数学源于生活,寓于生活,用于生活”的教育思想;突出了“特征让学生观察,思路让学生探索,方法让学生思考意义让学生概括,结论让学生验证,难点让学生突破,以学生为主体”的教学思路。例如:命题2 如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.
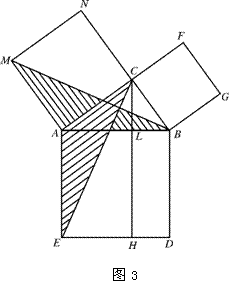
如下图,欲过基线MN上的一点C作它的垂线,可由三名工人操作:一人手拿布尺或测绳的0和12尺处,固定在C点;另一人拿4尺处,把尺拉直,在MN上定出A点,再由一人拿9尺处,把尺拉直,定出B点,于是连结BC,就是MN的垂线.
建筑工人用了3,4,5作出了一个直角,能不能用其他的整数组作出直角呢?
生:可以,例如7,24,25;8,15,17等.
3、在本节教学活动过程中,我经常走下讲台,到学生中去,以学生身份和学生一起探讨问题。用一切可能的方式,激励回答问题的学生,激发学生的求知欲,使师生在和谐的教学环境中零距离的接触。课堂上学生们的思维空前活跃,发言的人数不断增多,学生能从多角度认识问题,争先恐后地交流不同的意见和方法,收到比较好的效果。这是本节课的特色。
二、本节课的不足之处及改进方法:
1、本节课我没有利用多媒体辅助教学,如学习目标的发展、习题训练内容的展示、学生活动的要求、作业布置等,这些内容都是为教学服务的。如果用多媒体课件的展示,可以增大了教学密度,使学生的双基训练得到了加强,使传统的课堂走向了开放,使学生真正感受到学习方式在发生变化。在以后的教学中我应加强。
2、在重难点的突破上还应加一些递进的习题,降低题的难度,使优生学好,中等生也能跟上。在以后教学中,我会不断地更新教育理念,结合学生的认知规律、生活经验对数教材进行再创造,选取密切联系学生现实生活和生动有趣的数学素材,为学生提供充分的数学活动和交流的空间,真正把创造还给学生,让学生动起来,让课堂焕发新的活力。
反思二:
万事开头难,开学近20天以来,高效课堂的理念吹遍了我市的每一座学校,我也在魂牵梦绕中不断地摸索着,实验着。今天我作为我校的排头兵,上了一节展示课,其实不敢说展示课,只能是一节实验课,真是感觉压力很大。上完课后,有一种莫名的轻松。【勾股定理的逆定理教学反思5篇】。轻松之余对本课节的教学进行一些反思。
这次展示课,我上的是八年级数学课《17.2勾股定理的逆定理》,我是根据“五步三查”课堂模式来设计“导学案”和组织教学的。 这次课相对于过去基础上的课堂改革是完全不同的课,其进步之处之一是规范了课堂的结构,明确了课堂模式“五步三查”,操作上更能心中有数。进步之二是发挥学生的积极性方式与手段更多些,“老师需要什么?就评价什么”,进行了有益的尝试,将评价纳入整个课堂,如何通过开展小组的评比与竞赛调动学生积极性及学习氛围积累了经验。进步之三是“导学案”的编写上更适和学生,更有利于对课堂的指导。进步之四是课堂效率和课堂效果更好。进步之五学生的主体作用得到了真正的体现。进步之六是课堂不仅成了学习知识的地方,更是增进情感、培养能力的地方。
这次展示课也有待改进的地方,其一是“五步三查”模式操作细节不清楚,对整个操作流程理解不到位,导致整个课堂有些乱,因不能多讲,又不放心学生学。其二是学生的能力培养还应下大功夫,过去是以老师讲为主,学生只是听记,现在要他们自学、讨论,同学们还不习惯,导致课堂有些沉闷。其三是时间紧,教学任务完不成,课堂的知识掌握度、能力目标达成度较低。其四是“五步三查”各细节的科学性、有效性落实,有许多细节的落实与协调有待深化,如如何评价?如何有效利用评价得分?如何有效独学?其五是“导学案”如何更科学编制?体现分层同时又能更有利于指导学生的学,也有利于指导教师的教。其六更主要的是老师的观念,树立学生为主体的观念,将学生发展落实到教育教学各环节这才是根本。勇于变革和创新,积极研究和实践才能保障我们的课堂改革更顺利推进。【勾股定理的逆定理教学反思5篇】。虽然存在这样多,或更多的问题,但对其前景我们每一个人都充满了信心,我们相信只有这样做才能真正达到教育的目标。
反思三:
在十年的教学生涯中,我常常思考:怎样才能培养和发展学生的创新能力,增强学生的创新意识呢?
首先,教师自己要有创新的意识和创新的精神。就拿教材来说吧,教师不要把教材当作本本,当成一成不变的知识,原封不动地灌输给学生,而要根据学生的具体情况,采取不同的教学方式、方法,创造性地和有选择性地利用和处理教材,设计出符合学生实际情况的教学过程。但其指导思想不能变,那就是有利于基础知识、基础技能的掌握和学生创新能力的培养,能最大程度地使教学设计过程面向全体学生,充分照顾不同层次的学生,使设计的思路符合新课程倡导的理念。
总之,教师不要把数学教育单纯地理解成知识的传授和技能的训练。照本宣科,抱残守缺,是培养不出创新人才的。进行以探究为主的课堂教学,就是创新教学方式的一种。这种方式,可适用于定理、性质、法则、高尚以及一些数学规律的学习。因为,学生进入社会后,几乎很少直接用到数学中的某个定理和公式,但数学教学中所体现出的思想、方法以及善于合作交流,敢于探索的精神,却是人们一生中长期受用的。
《勾股定理的逆定理》这节课的教学,我采用了体验探究的教学方式。在课堂教学中,我首先创设情境,提出问题;再让学生通过画图、测量、判断、找规律,猜想出一般的结论;然后由学生想、画、剪、叠,去验证结论......使学生自始至终感悟、体验、尝试到了知识的生成过程,品尝到成功的乐趣。这不仅使学生学到获取知识的思想和方法,同时也体会到在解决问题的过程中与他人合作的重要性,而且为学生今后获取知识以及探索、发现和创造打下了良好的基础,更增强了学生敢于实践、勇于探索、不断创新和努力学习数学知识的信心和勇气。
要想真正搞好以探究活动为主的课堂教学,必须掌握多种教学思想、方法和教学技能,不断更新与改变教学观念和教学态度,使课堂真正成为学生既能自主探究,师生又能合作互动的场所,培养学生成为既有创新能力,又能适应现代社会发展的公民。
作为教师,在课堂教学中要始终牢记:学生才是学习的主体,学生才是课堂的主体;教师只是课堂教学的组织者、引导着和合作者。因此,课堂教学的设计,也必须体现出学生的主体性。
反思四:
本节课以活动为主线,通过从估算到实验活动结果的产生让学生总结过程,最后回到解决生活中实际问题,思路清晰,脉络明了。
例如:活动1问题:据说古埃及人用下图的方法画直角:把一根长蝇打上等距离的13个结,然后以3个结,4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
这个问题意味着:
1、如果围成的三角形的三边分别为3、4、5.那么围成的三角形是直角三角形.
2、体现了“数学源于生活,寓于生活,用于生活”的教育思想;突出了“特征让学生观察,思路让学生探索,方法让学生思考,意义让学生概括,结论让学生验证,难点让学生突破,以学生为主体”的教学思路。同学们经过操作,观察,探究,归纳得到直角三角形的判定,由感性认识上升到理性认识,能力得到提升。【勾股定理的逆定理教学反思5篇】。
3、在教学活动过程中,我经常走下讲台,到学生中去,以学生身份和学生一起探讨问题。用一切可能的方式,激励回答问题的学生,激发学生的求知欲,使师生在和谐的教学环境中零距离的接触。课堂上学生们的思维空前活跃,发言的人数不断增多,学生能从多角度认识问题,争先恐后地交流不同的意见和方法,收到了比较好的效果。
反思五:
星期五下午第一节讲了《勾股定理逆定理》第一课时,课后效果和我预想的一样,由于探究内容偏多,课堂容量大,后半部分感觉仓促,留给学生的思考时间显得不足。
回头反思,这节课的设计思路比较合理:定理来源于生活,服务于生活。我由勾股定理引出一道生活实际问题,引起学生的求知欲,然后和学生分三种方法探究,得出“勾股定理逆定理”,经过课堂练习夯实基础,最后利用新知解决开课时提出的生活实际问题,首尾呼应,学以致用。
对互逆命题,原命题,逆命题,互逆定理,逆定理等概念的讲解可随题点化,而详细讲解、随堂练习可做为第二课时的重点,让出更多时间来做勾股定理逆定理的相应练习,特别是应加大有灵活度和难度生活习题的练习,拓宽学生知识面,提高学生的发散思维能力。
总之,课堂设计要做到一个“狠”字,该删除的就删,教学目标不可贪多。我们围绕授课重点做相应探究,练习,次重点可放在下个课时重点讲解,探究时间要预留充足,相应练习宁精勿多,注重双基才是根本。
 爱华网
爱华网