★第二课时<?xml:namespace prefix =o ns ="urn:schemas-microsoft-com:office:office" />
[复习巩固]
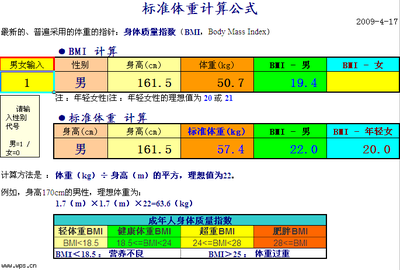
[投影]1.已知某<?xml:namespace prefix =st1 ns ="urn:schemas-microsoft-com:office:smarttags" />1 LH2SO4溶液中含有250 mL浓H2SO4,可以算出这种溶液的吗?(不能)
2.已知每100克H2SO4溶液中含有37克H2SO4,可以算出这种溶液的吗?(不能)
[设问]那么,要算出溶液中溶质的,必须从哪方面着手呢?
[结论]必须设法找出溶液的体积和溶液中溶质的物质的量。
[教师]请大家根据刚才的分析,做如下练习。
[投影]3.将质量为m,相对分子质量为Mr的物质溶解于水,得到体积为V的溶液,此溶液中溶质的为(c=<?xml:namespace prefix =v ns ="urn:schemas-microsoft-com:vml" />)
[引言]上节课我们知道了的概念及其与质量分数的区别,本节课我们来学习与溶质的质量分数之间的联系及有关溶液稀释的计算。
[板书]二、溶液中溶质的质量分数与的换算
[投影]例1.已知37%的H2SO4溶液的密度为1.28 g・cm-3,求其。
[分析]从上节课的知识我们知道,溶质的质量分数和都可用来表示溶液的组成。因此,二者之间必定可以通过一定的关系进行换算。根据我们刚才的讨论分析可知,要算出,必须设法找出所取溶液的体积及其中所含溶质的物质的量。由于浓度是与所取溶液的多少无关的物理量,所以,我们既可取一定质量的溶液来计算,也可取一定体积的溶液来计算,为此,我们可以采用以下两种方法。
解法一:
取100 g溶液来计算
m(H2SO4)=100 g×37%=37 g
n(H2SO4)==0.37 mol
V(液)==78.12mL=0.078 L
c(H2SO4)==4.8 mol・L-1
答:37%的H2SO4溶液的为4.8 mol・L-1。
解法二:
取1 L溶液来计算
V(液)=1 L
m(H2SO4)=V[H2SO4(aq)]・ρ・w=1000 mL×1.28 g・cm-3×37%=473.6 g
n(H2SO4)==4.8 mol
c(H2SO4)==4.8 mol・L-1
答:37%的H2SO4溶液的为4.8 mol・L-1。
[思考题]对于溶质质量分数为w,密度为ρ的某溶质的溶液,其的表示式为:
。
[同学们思考后]
[板书]c=
[练习]市售浓H2SO4中,溶质的质量分数为98%,密度为1.84 g・cm-3。计算市售浓H2SO4中,H2SO4的。(c==18.4 mol・L-1)
[设问过渡]如果已知溶液中溶质的c及溶液的密度ρ,又怎样求其质量分数呢?
[同学们对上式推导后得出]
[板书]w=
[投影]例2.已知75 mL 2 mol・L-1NaOH溶液的质量为80克,计算溶液中溶质的质量分数。
[分析]在已知溶液质量的情况下,要求溶质的质量分数还须算出溶液中溶质的质量,依题意,
我们可进行如下计算:
解:75 mL 2mol・L-1NaOH溶液中溶质的物质的量为:
n=c(NaOH)・V[NaOH・(aq)]=2 mol・L-1×0.075 L=0.15 mol
m(NaOH)=n(NaOH)・M(NaOH)=0.15 mol×40 g・mol-1=6 g
w(NaOH)=×100%=×100%=7.5%
答:溶液中溶质的质量分数为7.5%。
[教师]根据以上的计算,请同学们找出下列各量之间的关系。
[板书]
溶质的质量溶质的物质的量
溶液的质量溶液的体积
[学生们完成上述关系后]
[过渡]在实际生产中,对一定的浓溶液,还往往需要稀释后才能使用。如喷洒农药时,须把市售农药稀释到一定浓度才能施用,实验室所用一定浓度的稀H2SO4也均由浓H2SO4稀释而来,这就需要我们掌握有关溶液稀释的计算。
[板书]三、有关溶液稀释的计算
[设问]溶液在稀释前后,遵循什么样的规律呢?请同学们根据初中学过的一定质量分数的溶液稀释时所遵循的规则来分析稀释一定的溶液所遵循的规律。
[大家思考,学生回答]
[教师总结]稀释浓溶液时,溶液的体积要发生变化,但溶质的量(质量或物质的量)均不变。为此,在用一定的浓溶液配制稀溶液时,我们常用下面的式子来进行有关计算:
 爱华网
爱华网