函数中,有一种多项式函数形如y=ax^2+bx+c(a,b,c是常数,a≠0),最高次数是2,这种函数,我们称之为二次函数。二次函数知识点颇多,初高中都会出现,在初中,刚刚出现在一次函数数形结合学习之后,因此,二次函知识点离不开数形结合思想。
二次函数主要有哪些知识点?
二次函数知识点汇总及详细剖析 1、
定义与定义表达式
一般地,自变量x和因变量y之间存在如下关系:
y=ax^2+bx+c(a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.)
则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
二次函数知识点汇总及详细剖析 2、
二次函数的三种表达式
一般式:y=ax^2;+bx+c(a,b,c为常数,a≠0)
顶点式:y=a(x-h)^2;+k[抛物线的顶点P(h,k)]
交点式:y=a(x-x1)(x-x2)[仅限于与x轴有交点A(x1,0)和B(x2,0)的抛物线]
注:在3种形式的互相转化中,有如下关系:
h=-b/2ak=(4ac-b^2;)/4ax1,x2=(-b±√b^2;-4ac)/2a
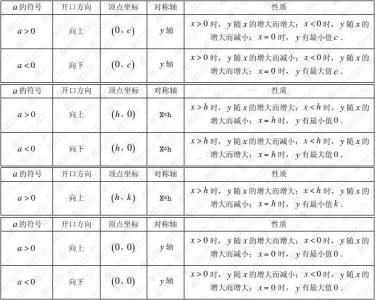
二次函数知识点汇总及详细剖析 3、
二次函数的图像
在平面直角坐标系中作出二次函数y=x2的图像,
可以看出,二次函数的图像是一条抛物线。
二次函数知识点汇总及详细剖析 4、
抛物线的性质
1.抛物线是轴对称图形。对称轴为直线
x=-b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
特别地,当b=0时,抛物线的对称轴是y轴(即直线x=0)
2.抛物线有一个顶点P,坐标为
P[-b/2a,(4ac-b^2;)/4a]。
当-b/2a=0时,P在y轴上;当Δ=b^2-4ac=0时,P在x轴上。
3.二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
|a|越大,则抛物线的开口越小。
4.一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时(即ab>0),对称轴在y轴左;
当a与b异号时(即ab<0),对称轴在y轴右。
5.常数项c决定抛物线与y轴交点。
抛物线与y轴交于(0,c)
6.抛物线与x轴交点个数
Δ=b^2-4ac>0时,抛物线与x轴有2个交点。
Δ=b^2-4ac=0时,抛物线与x轴有1个交点。
Δ=b^2-4ac<0时,抛物线与x轴没有交点。
二次函数知识点汇总及详细剖析 5、
二次函数与一元二次方程
特别地,二次函数(以下称函数)y=ax^2;+bx+c,
当y=0时,二次函数为关于x的一元二次方程(以下称方程),
即ax^2;+bx+c=0
此时,函数图像与x轴有无交点即方程有无实数根。
函数与x轴交点的横坐标即为方程的根。
画抛物线y=ax2时,应先列表,再描点,最后连线。列表选取自变量x值时常以0为中心,选取便于计算、描点的整数值,描点连线时一定要用光滑曲线连接,并注意变化趋势。
二次函数知识点汇总及详细剖析 6、
二次函数解析式的几种形式
(1)一般式:y=ax2+bx+c(a,b,c为常数,a≠0).
(2)顶点式:y=a(x-h)2+k(a,h,k为常数,a≠0).
(3)两根式:y=a(x-x1)(x-x2),其中x1,x2是抛物线与x轴的交点的横坐标,即一元二次方程ax2+bx+c=0的两个根,a≠0.
说明:(1)任何一个二次函数通过配方都可以化为顶点式y=a(x-h)2+k,抛物线的顶点坐标是(h,k),h=0时,抛物线y=ax2+k的顶点在y轴上;当k=0时,抛物线a(x-h)2的顶点在x轴上;当h=0且k=0时,抛物线y=ax2的顶点在原点
如果图像经过原点,并且对称轴是y轴,则设y=ax^2;如果对称轴是y轴,但不过原点,则设y=ax^2+k
二次函数知识点汇总及详细剖析 7、
定义与定义表达式
一般地,自变量x和因变量y之间存在如下关系:
y=ax^2+bx+c
(a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下。IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大。)
则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
x是自变量,y是x的函数
二次函数的三种表达式
①一般式:y=ax^2+bx+c(a,b,c为常数,a≠0)
②顶点式[抛物线的顶点P(h,k)]:y=a(x-h)^2+k
③交点式[仅限于与x轴有交点A(x1,0)和B(x2,0)的抛物线]:y=a(x-x1)(x-x2)
以上3种形式可进行如下转化:
①一般式和顶点式的关系
对于二次函数y=ax^2+bx+c,其顶点坐标为(-b/2a,(4ac-b^2)/4a),即
h=-b/2a=(x1+x2)/2
k=(4ac-b^2)/4a
②一般式和交点式的关系
x1,x2=[-b±√(b^2-4ac)]/2a(即一元二次方程求根公式)
二次函数知识点总是与图形相对应,这也是函数的特点之一,我们在学习二次函数的时候,一定要注重代数与几何的双重锤炼,做到真正的数形结合,同时,也能够让自己对二次函数知识点理解更深刻。
 爱华网
爱华网