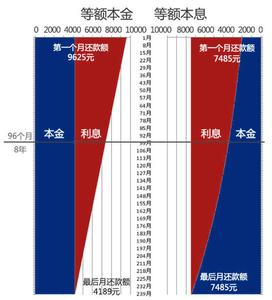
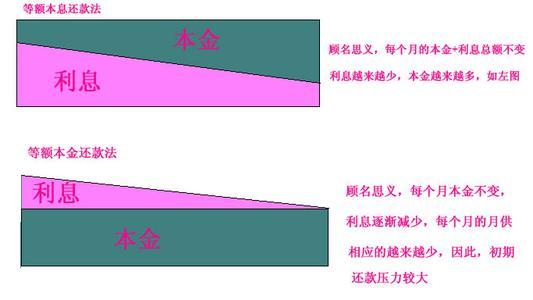
一、等额本息
设贷款额为a,月利率为i,年利率为I,还款月数为n,每月还款额为b,还款利息总和为Y
1:I=12×i
2:Y=n×b-a
3:第一月还款利息为:a×i
第二月还款利息为:〔a-(b-a×i)〕×i=(a×i-b)×(1+i)的1次方+b
第三月还款利息为:{a-(b-a×i)-〔b-(a×i-b)×(1+i)的1次方-b〕}×i=(a×i-b)×(1+i)的2次方+b
第四月还款利息为:=(a×i-b)×(1+i)的3次方+b ……
第n月还款利息为:=(a×i-b)×(1+i)的(n-1)次方+b
求以上和为:Y=(a×i-b)×〔(1+i)的n次方-1〕÷i+n×b
4:以上两项Y值相等求得
月均还款b=a×i×(1+i)的n次方÷〔(1 +i)的n次方-1〕
支付利息Y=n×a×i×(1+i)的n次方÷〔(1+i)的n次方-1〕-a
还款总额n×a×i×(1+i)的n次方÷〔(1+i)的n次方-1〕
二、等额本金
设贷款额为a,月利率为i,年利率为I,还款月数为n,an第n个月贷款剩余本金a1=a,a2=a-a/n,a3=a-2*a/n...以次类推 还款利息总和为Y
每月应还本金:a/n
每月应还利息:an*i
每期还款a/n +an*i
支付利息Y=(n+1)*a*i/2

还款总额=(n+1)*a*i/2+a
 爱华网
爱华网