因式分解(二次因式分解)是中学生数学的一项基本考察能力和技能。本经验将通过实例讲解如何用快速用十字交叉法来分解因式。
因式分解之十字交叉法(二次因式分解)――工具/原料纠结因式分解的学生
因式分解之十字交叉法(二次因式分解)――二次项系数为1的情况因式分解之十字交叉法(二次因式分解) 1、
二次项系数为1的标准情形如下,其中a和b可以是正整数、负整数或者0。
因式分解之十字交叉法(二次因式分解) 2、
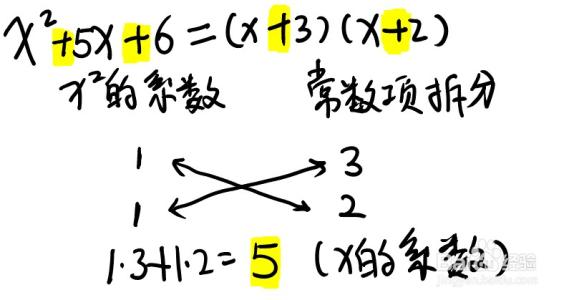
上面图片等号右方的(X+a)(X+b),从分解的因式正向运算来看是下面的结果,大家先看图,然后下一步总结规律。
因式分解之十字交叉法(二次因式分解) 3、
总结起来:(X+a)(X+b)中a+b的和会成为X一次项的系数,ab的积会成为常数项。所以这种因式分解的关键就是:将常数项分解成两个数字的乘积,然后其和等于一次项X的系数。
因式分解之十字交叉法(二次因式分解)_十字交叉法
因式分解之十字交叉法(二次因式分解) 4、
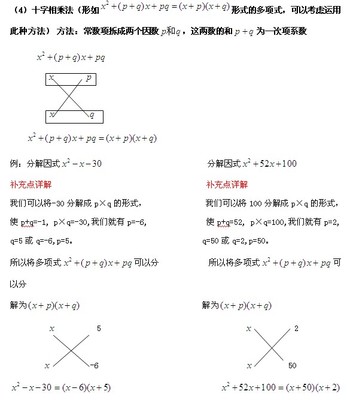
常数项为负数经典的拆解法如:-6=-2*3或者-6=2*-3,也就是常数项是一个绝对值较大的负数,而一次项的系数是一个绝对值较小的正数或者负数,如下例题:
因式分解之十字交叉法(二次因式分解) 5、
常数项为正数时类似,如下图:
注意:常数项是正数的时候可以拆解为两个正数的积,也可以拆解成两个负数的积。主要看一次项的符号。
因式分解之十字交叉法(二次因式分解)_十字交叉法
因式分解之十字交叉法(二次因式分解) 6、
总结二次项系数为1的情况分解因式规律:
1)拆分常数项成两个数字的积,和等于一次项X的系数;
2)常数项为负数,拆分成一个正数和一个负数的积,如果常数项符号为正,那么拆分数字正数绝对值要大,反之亦然;
3)常数项为正数,可拆分成两个正数或两个负数,符号也是看常数项的系数符号。
因式分解之十字交叉法(二次因式分解)――二次项系数不为1的情况:因式分解之十字交叉法(二次因式分解) 1、
二次项因数为1的情况下,十字拆分方法是一样的,不过还要将二次项也进行拆分。
因式分解之十字交叉法(二次因式分解)_十字交叉法
因式分解之十字交叉法(二次因式分解) 2、
总结二次项系数不为1的情况分解因式规律:
1)二次项也要进行拆分,和常数项拆分数字分别相乘并求和;
2)常数项是正数的情况,拆分数字符号与一次项系数一致;
3)常数项是负数的情况,拆分数字结果乘积之和与一次项系数一致。
因式分解之十字交叉法(二次因式分解) 3、
当X平方的系数为负数,可以先提取出符号再拆分,或者直接按照系数为负数直接拆分也可以。
因式分解之十字交叉法(二次因式分解)――注意事项如果您觉得此经验有用,可以点击本页面右上方的【大拇指】图案或者【分享】按钮,也可以点击本注意事项下方的【收藏】按钮。
 爱华网
爱华网