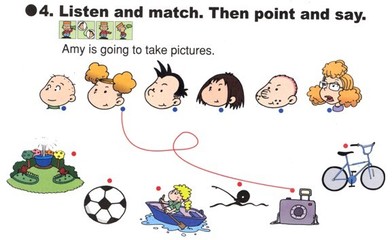
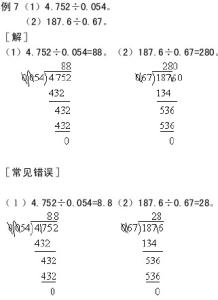
流水问题就是船在水中航行的行程问题。它有几种速度:
静水速度,船本身的速度,即船在静水中航行的速度。
水流速度,水流动的速度,即没有外力的作用水中漂浮的速度。
顺水速度,当船航行方向与水流方向一致时的速度。
逆水速度,当船航行方向与水流方向相反时的速度。
它们的关系如下:
顺水速度=静水速度+水流速度
逆水速度=静水速度–水流速度
例1、两码头相距108千米,一艘客轮顺水行完全程需要10小时,逆水行完全程需要12小时。求这艘客轮的静水速度和水流速度。
1、 顺水速度:108÷10=10.8千米
2、 逆水速度:108÷12=9千米
3、 静水速度:(10.8–9)÷2=9.9千米
例2、一客轮顺水航行320千米需要8小时,水流速度每小时5千米。逆水每小时航行多少千米?这一客轮逆水行完全程,需要用几小时?
要求逆水速度,需要知道顺水速度和水流速度;知道了逆水速度,就可求得行完全程所需时间。
1、 顺水速度:320÷8=40千米
2、 逆水速度:40-15×2=10千米
3、 逆水行完全程,需用几小时:320÷10=32小时
例3、某往返于甲乙两港,顺水航行每小时行15千米;逆水航行每小时行12千米,已知顺水行完全程比逆水少用2小时,求甲乙两港的距离。
顺水行完全程比逆水少用2小时,就是说,逆水行完全程多用2小时。行完全程逆水比顺水12×2=24千米。顺水每小时比逆水快15-12=3千米,由此,求得顺水行完全程所需时间,进而求得两港的距离。
15×[12×2÷(15–12)]=120千米
例4、 甲船逆水航行360千米需18小时,返回原地需10小时;乙船逆水航行同样一段距离需15小时,返回原地需多少小时?
由题中甲船逆水、顺水航行的距离和时间,可以求得甲船速度与水速的和及差,从而可以求出水速。
由乙船逆水航行的距离和时间,可以求得乙船在逆水中的速度;由乙船逆水速度水速可以求得乙船顺水速度,从而求得乙船返回原地需要的时间。
1、 甲船的顺水速度
360÷10=36千米
2、 甲船的逆水速度
360÷18=20千米
3、 水流速度
(36-20)÷2=8千米
4、 乙船逆水速度
360÷15=24千米
5、 乙船顺水速度
24+8×2=40千米
6、 乙船返回原地时间
360÷40=9小时
例5、 AB两港相距120千米,甲乙两船从AB两港相向而行6小时后相遇。甲船顺水航行,甲船比乙船多行48千米,水速每小时1.5千米。求甲乙两船的静水速度。
要求甲乙两船的静水速度,只需求出甲乙两船的静水速度的和与静水速度的差。
1、 甲船顺水速度与乙船逆水速度的和
120÷6=20千米
2、 甲乙两船静水速度的和
甲顺水速度+乙逆水速度=(甲静水速度+1.5)+(乙静水速度-1.5)= 甲静水速度+乙静水速度=20千米
3、 甲船顺水速度与乙船逆水速度的差
48÷6=8千米
4、 甲乙两船静水速度的差
甲顺速-乙逆速=(甲静速+1.5)-(乙静速-1.5)=甲静速-乙静速+1.5×2=8
甲静速-乙静速、8-1.5×2=5千米
5、 甲船的静水速度。
(20+5)÷2=12.5千米
6、 乙船的静水速度
(20-5)÷2=7.5千米
 爱华网
爱华网