系列专题:《教你如何降低炒股风险:零风险博弈》
图2-4-3 金字塔建仓数学模型图 2. 金字塔建仓对冲数学模型 (1)二路对冲数学模型 把总资金平分成两份,一份用于买进股票(建多头仓),一份用于卖出股票建空头仓。 确保多头和空头资金是用不完的,资金无限大。 当股价不断地下跌,不断地建多头单,总有资金建多头仓。当股价不断地上升,不断地建空头单,总有资金建空头单。 (2)高点二路对冲数学模型 在股价处在历史最高位时,买进1手股票(建多头单),卖出空头总资金股票(建空头单)。 当股价下跌时,按直线方程式买进股票(建多头仓),同时按直线方程式平空头股票(平空头仓)。
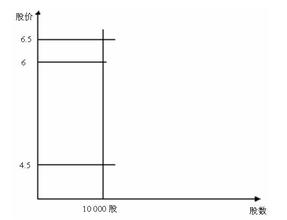
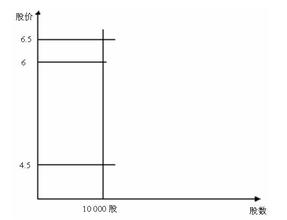
图2-4-4 金字塔建仓对冲数学模型 (3)低点二路对冲数学模型 在股价处在历史最低位时,卖出1手股票(建空头单),买进多头总资金股票(建多头单)。 当股价上升时,按直线方程式平多头股票(平多头仓),同时按直线方程式建空头仓。 当股价单边下跌、单边上涨和股价出现震荡,这种金字塔建仓对冲数学模型都能赢利。 (三)均分建仓数学模型 1. 均分建仓数学模型 建仓时是用上面的直线方程来计算买入多少股票数,在直线上分多少点可以由读者自己决定。可以分5点,也可以分10点等。 如图2-4-5所示,在6.5元到4.5元之间分8点,当股价在6.5元时,买入股票1000股。当股价每跌0.25元,加仓买入1000股;当股价不断向下跌时,均等买入的股票数越来越多,股票的成本是均匀分布在股价的纵坐标上,我们称之为均分建仓数学模型。 图2-4-5 均分建仓数学模型图 2. 均分建仓对冲数学模型(网格对冲交易模型) 二路对冲数学模型。 把总资金平分成两份,一份用于买进股票(建多头仓),一份用于卖出股票建空头仓。 把每份资金按从历史最高价到历史最低价分成N份。 当股价不断地下跌,不断地建多头单,总有资金建多头仓。当股价不断地上升,不断地建空头单,总有资金建空头单。 图2-4-6 均分建仓数学模型 (四)单边交易的风险与对冲交易的风险比较 1. 单边交易的风险在金融产品价格的单边上涨和下跌 如果你是做多头,当金融产品价格下跌,投资者发生投资损失,损失的大小和单边下跌的幅度成正比。 如果你是做空头,当金融产品价格上升,投资者发生投资损失,损失的大小和单边上升的幅度成正比。 2. 对冲交易的风险在于数学模型的设计和历史最高价和最低价的确定 当股价往上升并突破历史最高价格,对冲交易将出现亏损,亏损是由于空头产生的。 当股价往下跌并跌破历史最低价格,对冲交易将出现亏损,亏损是由于多头产生的。当价格在历史最高位和最低位波动中变动,对冲交易的风险是零,是正收益。 要防止出现对冲交易的风险和得到对冲收益最大化,交易数学模型非常重要,在确定最高价和最低价时要留有保险系数,保险系数的大小取决于用户的设计和对风险的承受能力。 3. 单边交易收益与对冲交易的收益比较 当金融产品的价格单边上升和单边下跌,投资者在做单边交易时,如果方向做对,单边交易的收益要大于对冲交易的收益。当金融产品的价格出现震荡,对冲交易的收益大于单边交易的收益。
 爱华网
爱华网