如果我们重复地从平均数μ,标准差为σ的母群中抽取样本大小为N的许许多多样本,得到许许多多样本平均数,而这些样本平均数将成为常态分配,不管原来母群的各分数之次数分配形状如何,且这些样本平均数的平均数将等于μ,这些样本的标准差(特称为标准误) 将等于σ/√n.

另一种解释: 母群是一个有着母群平均数μ,标准差σ的母群。我们从该母群中随机取n多个样本。这些样本的平均数我们用Xn表示。如果我们按上述过程做一次的话,得到的Xn是一个具体数字。但Xn实际上也是一个随机变量。它也有自己的概率分配。我们把这个随机变量Xn的期待值E(Xn)或平均值表达为μXn,把它的标准差表达为σXn。中央极限定理告诉我们这个随机变量Xn的分配是常态分配。并且期待值μXn就等于原来母群的平均数μ,标准差也跟原来母群标准差有关,σXn=(σ^2)/n。
爱华网本文地址 » http://www.aihuau.com/a/9101032201/291980.html
更多阅读
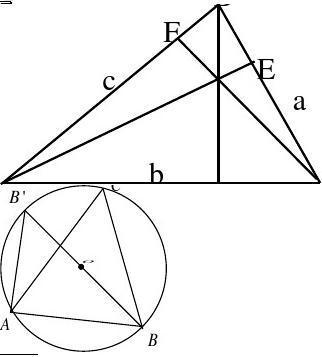
在备课中有两个问题需要精心设计.一个是问题的引入,一个是定理的证明.课本通过一个实际问题引入,但没有深入展开下去;对正弦定理的证明是利用三角形的面积公式导出的,但不够自然.为了处理好这两个问题,我首先确定了一个基本原则,就是充分

哥德巴赫猜想证明与对称奇素数定理吕明进“任意大于4的偶数都可表为两个奇素数之和”的哥德巴赫猜想,自1742年一提出,国际上就有许多著名数学家力求攻克它,但直至20世纪20年代,进展甚微,均未获得成功。因此,英国著名数学家哈代于1921年

相信对任何一个喜爱钻研的学生来讲,最无法接受的事情是:被别人抛给一个公式,并被告知公式你现在尽管用,但公式的道理以你现在的水平没法跟你解释.我在学生时代就非常抵触这种做法,碰到任何之前没见过的数学结论,一定要想法设法证明它,否则总

1985年央视春节联欢晚会节目单主持人:马季(已故,2006年12月) 姜昆 张喻 朱苑宜(台湾) 斑斑(香港)总导演:黄一鹤第一组1.京戏:《百猴迎春》 演出单位:中国京剧院2.器乐演奏:《编钟乐曲》 演出单位:湖北省歌舞团3.歌曲:《南乡子》 演唱者:李元华4.

三色就能交于一点,五色不能交于一条线……有待思考原文地址:四色定理作者:wuqian四色定理四色定理地图四色定理(Four colortheorem)最先是由一位叫古德里(Francis Guthrie)的英国大学生提出来的。四色问题的内容是:“任何一张地图只用四

 爱华网
爱华网



