企业核心竞争力受到越来越多企业的重视,随着这一理论的成熟,很多企业都在实践中运用,并在研究企业战略的基础上建立起了自身的核心竞争力评价指标体系。然而如何更加科学的确定评价指标的权重并进行科学的评价一直困扰着很多企业。在本文中,笔者将以某乳制品企业建立的指标体系为例,利用层次分析法确定指标权重,并建立相应评价的数学模型,为企业解决这方面的问题提供示例。
一、评价指标比重的确定
指标体系的各层次中每一个指标,其重要性的程度是不尽相同的。正确地确定指标权重,对于准确地评价核心竞争力具有重要意义。指标权重的确定,可采用专家自接评定的方法,也可采用定性与定量相结合的层次分析法(AHP)等。
层次分析法((The Analytic Hierarchy Process,简称AHP)是美国著名运筹学家T. L. Saaty于70年代提出的一种系统分析方法。它是一种常用的多指标综合评价方法,已在许多领域得到广泛的应用。AHP方法的基本思想是:先根据问题的性质和要求所构成的总目标,将问题分解为相互联系的有序层次,使目标条理化;然后按照问题的结构层次从上而下,逐层确定同层次上各元素相对上一层支配元素的相对重要性:最后综合得到各层次元素相对于总目标的综合权重。
1.专家组人员构成:应选取对公司及乳品行业情况非常熟悉的人员参与评分。
2.判断矩阵的确定:根据前文已建立的核心竞争力评价指标体系,通过专家对各指标的重要性予以量化,构造判断矩阵。
为了使各个指标两两比较而得到量化的aij,引入aij的量化标度值(见表1)。
表1 标度值表
3.计算权重。
具体步骤如下:
步骤一:构造两两比较判断矩阵
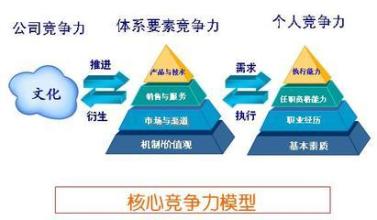
核心竞争力层次结构模型中,由高到低依次为A,B,C三层,A核心竞争力评价目标层,B层指准则层六个一级评价指标,C层指子准则层十七个二级评价指标。准则层B由六个因素B1、B2、B3、B4、B5、B6两两进行比较,以aij表示Bi与Bj对目标层A的影响之比,AB表示准则层B对目标层A的判断矩阵,于是我们可以得到两两比较判断矩阵。
AB= (aij)6×6(i,j=1,2,3,4,5,6)
判断矩阵应为正互逆矩阵,即应满足:
aij>0,aji=1/aij(i≠j),aii=1(i,j=1,2,3,4,5,6)
同理,可构造子准则层C的判断矩阵BC。
步骤二:层次单排序及其一致性检验
求解判断矩阵的最大特征值λmax及其所对应的特征向量W,W经过标准化后,即为同一层次中相应元素对于上一层中某个因素相对重要性的排序指标。
但是,指标成立的前提是构造矩阵需经过一致性检验。一致性检验是指检验所构造的判断矩阵是否满足一致性。一致性可定性地理解为人们构造判断矩阵时前后思维要保持连贯性、传递性。其准确的数学检验过程为:
第一步,计算 ,式中n为判断矩阵的阶数。
第二步,根据判断矩阵阶数,查出平均随机一致性指标RI(见表2)
表2 平均随机一致性指标RI
第三步,计算一致性比率:
若CR≤0.1,W即为同一层次中相应元素对于上一层中某个因素相对重要性的排序指标;否则,需重新构建判断矩阵,直至通过为止。
1.4综合评判的数学模型
对乳品企业核心竞争力状况的的评价,首先要充分了解企业的相关基本情况,并依据核心竞争力评价的指标体系对各指标值进行评定。为此,设计了一份进行该项调查的问卷,如表3。其中指标体系中的各项指标内容均以附页作补充说明,要求专家采取[0,1]分制的形式表示其对各指标的肯定程度。
表3 乳品企业核心竞争力综合评价调查表
 爱华网
爱华网