(续接上帖)
“三熵”对比之二。
同理,信息熵的概念也仅仅是因为香农在形式上把信息量定义为一个概率的对数形式,本质上和“克熵”毫无瓜葛。
“信息量I”是一个什么性质的变量?过程函数还是状态函数?很难界定。我们可以从一张照片上获得信息,也可以从一段录像当中获得信息。前者可以说是状态量——如果信息是客观存在的话;而后者是过程量——获取信息速度在时段上的积分。
“信息量”如何统计也是一个问题:是信息源发出的物理信号量?还是信息接受者接受到的物理信号量?还是接受者经过自己的加工综合分析后的结论?是静态的状态信息?还是动态的过程信息?这些问题都含而混之。
如果信息是人与物的互动关系的表示,信息就不是一种客观存在的,也是不可客观计量的主观东西。信息就不再属于外在事物的自身属性了。由此,信息熵同热温商和统计熵都不可类比,热温商描述了两个物系的关系,统计熵描述了一个事件自身的变化过程,而信息熵还涉及到观察者的状况。
如果用计算机传递的信息的0、1字符数计量信息量,它也仅仅是一个特定的翻译方式得到的。例如一个板上写上三个汉字,直接编码可以得到一组0、1数据;但是如果有人把它翻译为英语再行编码,得到的数据量和汉字的量就完全不同了,换个人翻译又是另一番模样了。如果信息量是接受者经过大脑加工之后的表达,则更加复杂。对一条原始信息用不同的密码进行加密后得到的传输信息量是完全不同的。例如一群人看同一部电影,观后感各不相同,有人说索然无味,有人百感交集,有人凑个热闹,有人看出了门道。前几日本·拉登又出来抨击美国了,美国的情报人员对拉登的胡子的兴趣很大,希望能从拉登的胡子上看出他藏身何处,而这个留着黑胡子的拉登形象在一般老百姓看来没有什么信息量,更不知道如何从中可以分析出拉登的行踪。
由此可以说,信息学尚处于一门“概念学科”的阶段,离成熟理论还相去甚远呢。
汉语“信息”一词只是“有用信号”的代名词,已经溶入了价值判断的因素,说“获得信息就是不确定度减少”也是没有道理的,信号有用无用是无法界定的,刑侦专家和普通人看到同一张照片获得的信息量是大不相同的。大量的虚假信息和战场上的信息战心理战,结果或者目的都是增加了对方的认识混乱,导致不确定性增加而不是减少。
不知道看官是否看过王朔的小说《各执一词》,如果没有看过最好去找来看一看,就知道什么叫做“越听越糊涂”了。这部小说描写的故事就是随着信息获取的增长导致判断的不确定性越来越大,以至于最终信息获取者(民警)竟然无法描述事实真相。在促使信息论发展的计算机时代,有位科学家就看到了信息的这种特征,预言说计算机不仅不能解决问题,而且会使人类面临的问题愈加复杂化。
经济学的“完全信息”是一个荒唐的假定,完全信息意味着无穷多信息,这是不可能的。交换双方的公平充其量只能定义在“信息对称”上,而不可能定义在“完全信息”之上。之所以说“充其量”,是因为信息量的大小和接收信息的人的信息处理能力是互动的,信息不是事物的客观内在属性。“对称”意味着默认交换双方对信息处理和再加工的能力,而这不是现实。
由于“信息”是事物与人之间的互动关系,因此,孤立的事物没有“信息”;如果不存在具有智能的生命,也没有所谓的“信息”。非智慧生命的事物之间只有质量和能量的传递和力作用,而没有“信息”。现代信息论用“确定性”来定义“信息”,然而,确定抑或不确定与确定者“人”有关,因人而异难以确定。物理学上与“熵”概念有关的关于“序”和能量“品位”的观点,这都是唯心主义的观点,是把人的价值判断融入到客观事实的研究当中的表现。从某种意义上,对自在自为的宇宙大自然来说,不存在确定性问题,或说一切都是确定的,所谓不确定性只是人类认识水平的“不可知”的表现而已。爱因斯坦也认识到上帝从来不掷骰子。
“负熵”的概念是物理学近些年来的热词,也源于“信息熵”的概念。但是,如果我们看一看其表达方式⊿I=-⊿S就知道问题所在了。⊿I=-⊿S的文字表达是“信息量欠缺=负熵(熵的减少)”,很显然,这里的“负熵”不是指在熵前面加一个负号,而是在“熵变”的前面加了一个负号。如果熵是作为一个状态函数存在,则熵变是过程函数,负熵,顾名思义应该是“-S”,按照变号不变性的逻辑规则,负熵“-S”还是一个状态函数,而“-⊿S”是一个过程函数。故而,“负熵”和“熵”不是许多人所理解的相对应的一对概念。把负熵当作和熵对应的概念把玩的人实则是对熵理论知之甚少。
把⊿I叫做“信息量欠缺”也与数学习惯格格不入,让人匪夷所思。按照数学习惯,⊿如果叫做“增”,则-⊿理所应当就是“减”,进而⊿I=-⊿S应该解读为“信息的增量=熵的减少”,但是信息学却出人意料地把⊿I叫做“信息量欠缺”。我们可以把⊿I=-⊿S作一个移号处理,变成-⊿I=⊿S,如果⊿I叫做“信息量欠缺”,则-⊿I就是“负欠缺”,理应叫做“信息量增加”,那么-⊿I=⊿S的意义就是“信息量的增加=熵的增加”,换句话说,信息和熵是对应的概念,而不是时髦的理论“信息是负熵”。大家可以感到,同一个数学表述当中,是如此的逻辑混乱。

退一步,如果“负熵”仅仅是“负熵变”的不恰当口误,那么“信息是负熵”的说法就更缺乏逻辑一致性了,应该说“信息增量是‘负熵变’”才对。
无论所谓的“统计熵”还是“信息熵”都是从研究事件概率入手的,或简言之都是研究“事件”的。而“事件”必对应于一个过程,有起点有终点有发展变化,涉及到时间变化即时段问题,所以,统计熵和信息熵的概念必然不能导出和作为状态函数的热温熵概念的对等联系。
顺便谈谈关于状态函数的性质划分问题。
状态函数有两种性质类型,一类叫做强度性质,一类称为容度性质。强度性质指与系统物质的量(数量、质量和体积)没有关系的性质,如温度T、压强P等等,是针对物系中任意一点的性质,又可以叫做“点性质”;而容度性质就是和物质量有关的性质,如体积V、尺度L、质量m等。
强度性质和容度性质的一个明显的区别就在于,前者不具有加和性和加和意义,而后者可以加和。例如,你不能够把两个系统(或一个物体上的两个点)的温度加起来求得一个“总温度”,也不能把两个容器当中的压强加起来求“总压强”。对于平衡态系统来说,体系内某强度性质是处处相同的。但是,你可以把两个物体的体积、尺度或者质量加起来求得总体积、总长度、总质量,其物理学意义十分清晰。体积和质量就是针对“容量”而言的,不存在某点的体积和质量这种情况(虚构的质点模型除外)。
由于流量(过程量)可以看作是运动的累积,或者说速度在时间上的累积,因此,流量都属于容量性质的变量。例如把一个过程分割为有限个段,则流量具有加和性。例如日用水量加起来就是周、月、季、年的用水量等等。
现实统计当中,有许多不顾变量性质的、人为设置的、意义极其含混的统计结论,如同数字游戏一般。由这些结论再总结出所谓的规律,常常误导人们的思维。
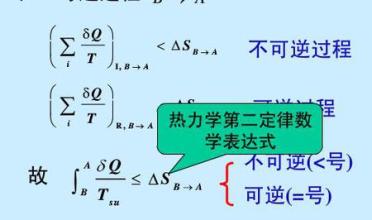
作为热温商的熵是什么性质的状态量?这个问题可不好回答,因为热温商概念本身不能成立,在继续探讨它是容量变量还是强度变量就毫无意义了。错误的热力学习惯认为热温商是一个容度性质的状态函数,但是,这种认识是不能成立的。
热力学认为熵是一个容度性质的状态量,理由是在式子⊿S=Q/T当中,因为流量Q是容量性质的,所以S就是容量性质。这种解释却是指东说西,完全驴唇不对马嘴,因为Q/T是“熵变⊿S”,而非熵S,得到的结论也应该是⊿S具有何种性质,而非S具有何种性质。热力学当中也只是把一个过程分成若干段把其熵变⊿S加和而非把熵S加总求和。
退一步来说,如果⊿S的性质仅仅因为⊿S=Q/T而Q是容量性质而定,那么我们对之做一个变形就是T=Q/⊿S,是不是也可以因此说T是容度性质的变量了?
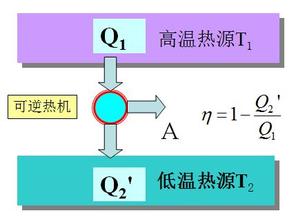
从统计学方面来说,假如像玻尔兹曼所述熵是序的一种度量(S=klnW),而序w是一个强度性质,即我们不能把两个系统的状态几率求和。我们能把一个处于平衡态的均相孤立系统人为分割为众多的部分,每一部分都是相同的,具有相同的“序”,即对应于一个统计熵状态,我们不能够把孤立系统的熵看作是这些部分的熵之和,否则,系统熵就随着分割的不同变成任意大小了。因此以波尔兹曼统计熵的思想来看,S=klnw应该是一个强度性质的状态函数,而不具有容度性质。例如对于图-5这个孤立系统,冷源的状态几率为W1,热源的状态几率为W2,我们就无法计算总系统的状态数究竟该是多少。
在经济学方面,价格是描述交换状态的,是一个状态函数(存量)。由于价格就是单价,所以是和绝对数量无关的一个强度性质的存量。因为价格是强度性质,所以不具有加和性,青菜的价格是1元/KG,就是说每一kg的索价都是1元,而不是说两kg青菜的价格就是每公斤两元;上午的红薯每斤一元,下午的红薯八毛一斤,你不可能把它们加起来求总价格。能够加总的是销售额和销售量,而不是价格。也正因为如此,早前的帖子才基于价格这种不可加和的强度性质说“德布鲁的那块诺贝尔奖牌一文不值”,显然,经济学一直没有认识到价格的存量特性和强度性质,导致把一般均衡理论建立在一个荒唐的价格加和运算基础之上。(请续看下帖)
 爱华网
爱华网