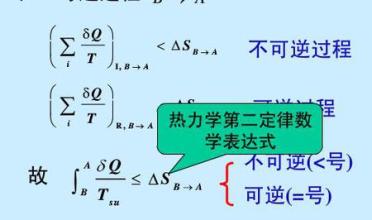
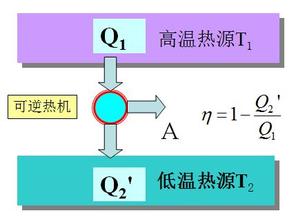
(续接上帖)
我们常用“变化”、“运动”、“过程”等术语描述事物运动,其实三种词语是三位一体的同义词。如果我们观测不到“变化”就无法确定运动的存在,也不能称其为“运动”,而任何运动和变化都必须假以“时间过程”来实现。“量变”就是指某一状态量在一个过程始末两点的状态改变,因此,“变量”若是态函数,对应于一个时点,则态函数的“量变”对应于由两个点(始末)确定的过程,是过程量。使用“过程”一词既可以单单意味着变化,也可以意味着描述路径,总之是针对一个完整的过程。
所以,如同状态函数分为两种一样,过程函数同样分为两种:一种单纯描述“变化”的,它只与过程的起始点的状态有关,考察的是状态的变化量即同一存量在起始两点上状态量的差值;另一种不仅仅描述变化,而且描述变化的中间过程,即不仅仅与起始点状态有关,还与路径有关。第一种谓之“点流量”,第二种谓之“积流量”。
同样,过程函数的两种类型在数学上的描述表现为:“点流量”简洁地表示为存量在起始点上的差额,如⊿S=S2-S1。而“积流量”表示为一个定积分,如∫f(t)dt从过程开始点a点积到终点b点,实际上也就是“流存量”的上限b被指定为终点(非变量化)后的结果。量变“⊿”已经涉及到从1到2两个状态点之间的变化问题,即涉及到由始末两点确定的一个运动过程,所以是过程函数而不是状态函数。

在微积分条件假定成立的基础上,在数学上“点流量”和“积流量”是统一的,即:
⊿S=S2-S1=∫12(dS/dt)dt,其中dS/dt为S流随时间t变化的速度函数。
“点存量”和“点流量”类比于“流存量”和“积流量”,前者都是后者的部分内容,后者包含着更加丰富的认知信息。“点存量”考察的是一个点的状态,“点流量”考察的是两个点的变化,“流存量”是考察两个指定点中间的任意状态,而“积流量”考察的是两点中间的完整过程的问题。
物理学界并没有认识到状态函数和过程函数的这种细分,以往学界对流量、存量的认识只是简单地局限于“点存量”和“积流量”。既没有人指出“流存量”的存在(往往是因为它涉及到状态点的历史过程而错误地将之当作流量),也没有人指出“点流量”属于流量的一种(往往是采取避而不谈其性质的态度)。例如,所有关于“熵”的概念,都是从熵变⊿S开始的,而不是直接定义“熵”S≡什么,同时热力学从来都避而不谈⊿S是状态函数还是过程函数(这个问题后边还要谈)。最新看到的某高校热学教材在讲解焦耳的内能定理U2-U1=W绝热时说:“因为W绝热仅与初态、末态有关,而与中间经历的是怎样的绝热过程无关,故内能是态函数。”显然作者在此陷入了迷茫,一句话前言不搭后语——既然是W绝热和过程无关,不顺乎逻辑地说W绝热是态函数,却话锋一转而说内能是态函数。作者没能理解到,既然涉及到一个过程的初末两个点,也就是涉及过程即与过程有关,任何状态函数都只能是针对一个状态点所在的时点而言的,不存在涉及多个时点的状态函数。因此⊿U=U2-U1就是一个过程函数,而W绝热=⊿U还是一个过程函数,保持了“功是过程函数”的认知逻辑一贯性,不论是否绝热过程。
同样,这本书在谈论第一定律U2-U1=Qin+Win(注:原文为Q+W。标注in表示输入系统的能,这种规定逻辑上比较一致。以往的书有以输出功为正的说法,此时应写为⊿U=Q-W)时刻意补充到:“功和热都与所经历的过程有关,它们不是态函数,但两者之和却成了仅与初末状态有关、而与过程无关的内能的改变量了”(《普通物理学教程·热学》第二版,高等教育出版社,秦允豪,2002,P179、P180)。
为此,作者还在章后的习题中布置了一道思考题:“功是过程改变量,它与所进行的过程有关,但为什么绝热功却仅与初末态有关,与中间过程无关?热量与进行过程有关,但为什么在定体条件下吸收的热量与中间过程无关?”(同上,P220,习题4.9)
同样的情况还出现在反应热和反应焓的表述中,密闭容器内的等容化学反应,吸、放的热量Qv=⊿U=U2-U1,压条件下化学反应吸放热Qp=⊿H=H2-H1,作者并没有就此评论说一个过程量(热Q)“却成了仅与初末状态有关、而与过程无关的内能(焓)的改变量了”。
显然,这里的问题和上面相同,即作者没有认识到⊿U(=U2-U1)、⊿H(=H2-H1)就是过程量,因为它已经涉及到一个具有明确起始点的变化过程,是“点流量”。作者没有意识到过程量并不单单指针对中间路径的。“始末两点”是确定一个“过程”的必备要素,与始末点有关就是与过程有关。这种表述和习题要确定的观念已经违背了同性质的不同变量运算的结果性质不变的变量逻辑,也与上述焦耳在内能定理中的表述冲突:既然反映能量守恒的第一定律是普适的,其中涉及到的功W不可能一会儿是状态量一会又是过程量。反过来,假如认识到⊿U、⊿H是过程量,就不会有以上的“感叹”,一切都顺理成章了。在一个状态点上没有功和热可言,或者说功和热必然涉及到一个状态变化过程,这一点足以用来说明和定义功和热的过程量性质。
【特别规定】一个流量在两个时段内的取值大小对比结果还是一个流量。此即:过程量F在过程1和过程2当中的取值分别是F1和F2,则变量F的量变为⊿F=F2-F1是一个流量,此流量因为涉及到两个过程,所以称其为“二级过程量”(二级流量)。“二级流量”也就是“变化的变化”。
【变量逻辑规则1:同性质的不同变量运算的结果性质不变。】
手边的一本旧高校教材对“状态函数”的讲解和三十年后的最新教材其实没有什么两样,说明物理学本身在这个问题上没有认识上的进步:
【确定系统状态的变数就是状态函数。热力学用系统的性质来确定系统的状态,所以这些性质也就是状态函数。当系统经历一过程时,状态函数的变化就等于终态数值减去始态时的数值,如温差⊿T=T终-T始;压差⊿P=P终-P始。】
【因此,尽管系统从始态变化到终态时可以采取不同的途径,但状态函数的变化,或如上所写⊿T、⊿P等状态函数的增量,只与系统的始态和终态有关,与途径是无关的。状态函数的这种重要性质在以后经常要用到。对于一个循环过程(注:系统从始态起经历了一系列的变化又回到了原来的状态的过程)来讲,系统由始态起,经过一系列的变化又回到了始态,则系统的状态函数的增量必然都等于零。】(《基本有机化学工程》,人民教育出版社,天津大学基本有机化工教研室编,1976,P44)
特别提醒几点:
第一,时间变量t本身是态函数,而且是“状态原函数”,因为状态就是针对时点而言的。
第二,时间段长度或说时间的增量⊿t(=t2-t1)是过程量,是“过程原函数”。正是因为t的存量本质和⊿t的流量本质,决定了与之对应的变量的性质;
第三,对一个变量的纯粹运算,如改变正负号、求微(d)、求对数(log、ln)、求倒数、改变计数方式(如%、科学记数法)等等,都不改变变量的性质。因此,如果某变量A是一个态函数,则-A、dA、1/A、logA、-lnA等等也依然是态函数。
对存量、流量的细分是认识论上的一大飞跃,完全理顺了有关流量存量的变量逻辑。
(请续看下帖)
 爱华网
爱华网