(续接上帖)
“三熵”对比之一。
在写本段帖子的时候,我们首先要对伟大的物理学家玻尔兹曼表示歉意,因为本帖的内容涉及到这位伟人的墓志铭的全部内容:S=klogW。但科学容不得我们含混地接受任何有疑问的东西。
所谓“三熵”,指从克劳休斯等式推演出来的所谓的“热温商”、玻尔兹曼用微观状态数表达的所谓的“统计熵”、以及香农的“信息熵”。“三熵”也可以依次称为“克熵”、“波熵”和“香熵”。科学史研究者认为,波氏统计熵的概念为克氏热温商概念找到了微观基础,而香氏信息熵概念的出现,使得本来就不成立的克熵概念看起来更加有鼻子有眼,熵概念愈发“科学化”而且用途广泛。但是下面要说的是,三熵之间并没有物理学意义上的任何关联,所谓统计熵、信息熵同“热温商”的关系纯属牵强附会生拉硬扯的形而上。
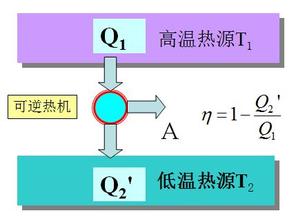
既然原始的热温商概念不可成立,则必不能够为之建立起一个合理的微观的统计物理学基础。波尔兹曼把系统的微观状态数W(有些教材写为Ω)用对数形式表达,这一点本身并没问题。用另一种计量方式表达一个变量并不改变这个变量的本质和性质,比如一个变量的计数可以用小数形式,也可以用百分数抑或科学记数法都是一样的。
或许统计学并没有注意到,“分布”其实有两种——存量的分布和流量的分布。存量分布或者是流量分布,判断的标准是看“分布基”的性质,分布基是状态量,则属于存量分布;分布基是过程量,则属于流量分布。
例如我们进行视觉测试的时候用的图片,其上的色点分布是固定的,我们可以计算每种颜色所占据的面积比例,也可以描述每种颜色在图案上的分布密度。但是色斑图像的总面积或点数是一个存量概念,我们测算的每种色点的数量、面积也是存量,所以,这种分布属于“存量分布”。再例如我们调查一片林子当中不同大小树径的树木的分布情况、一个年级的学生的身高分布情况等等,也都属于存量分布。存量分布是一个时点之上的分布,你可以用照相机在任意时点去拍下一张照片回去慢慢进行研究,最后得出某年某月某日某时某分某秒的分布是如何如何之结论。
但是,还有完全不同于存量分布的另一种分布,即“流量分布”。例如,研究国家某年出生的人数Nm(m表示年份)的地域分布。以行政县(编号为i=1、2、3……)为单位,每个县的当年出生人数Ni占总出生人口的比例为Ni/Nm。由于Nm、Ni都是流量,因此这种分布是“流量分布”。流量分布涉及到一个时间段,你必须用录像机把它纪录下来而不是用照相机拍下来才能研究。
统计物理学在这方面其实是含混的,它所默认的分布似乎就是流量分布而不是存量分布,如“打靶实验”、“咖尔顿板试验”和“朗缪尔分子射线束实验”等等都是流量分布研究,之所以说它们是流量分布,就说因为这种“分布”对应于一个过程,分布基是每轮实验中的总数量,而不是一轮实验当中的一个状态量,不是对应于一个时点。但是,统计物理学有序度、混乱度等等却都是状态特征的概念,因此说,统计物理学在方法层面还有很多问题存在。
我们可想而知,如果不区分分布的两种类型,从诸如“打靶实验”、“咖尔顿板试验”和“朗缪尔分子射线束实验”等流量分布研究是不可能得出一个和想象中的状态量“克熵”有关的结果的。
由于存在两种发布,所以,概率的概念其实也有两种——存量的概率和流量的概率。显然,存量分布和流量分布其概率都可以满足所谓的“归一化”,如ΣNi/Nm=1。
“微观状态数”是一个含混的概念。首先,我们从各种关于玻尔兹曼统计物理学的教材当中,都无法确认微观状态数的含义和统计方法,并由此进一步确定微观状态数W的变量性质。在“咖尔顿板试验”或者“朗缪尔分子射线束实验”当中,总数N其实都是一个流量性质的常数,是和实验序次对应的某个时段内的总粒子数,而不是一个和时点对应的变量。因此,麦克斯韦速度分布表达式的正确写法应该是dN/(N0dv),而非dN/(Ndv),也就是说,总数N0在微积分运算过程中不是变数N而是常数。
例如物理学教材总是把粒子在位置上的数量分布作为“状态”,其实状态还有自旋方向之分,例如张三李四在A房间,王五马六在B房间,这只能算是一类分布,还可以按照张三李四、王五马六在各自房间中的面向和运动方式细分下去,所以微观状态数是无穷尽的。即便是仅仅按照位置参数确定状态数,由于一个体积V内的位点数是无穷的,所以微观状态数还是无穷尽的,即W=W(x,y,z,t)的取值是连续无穷多的。也就是说,任何一个大数粒子系统,其微观状态数都是无穷大的——你可以用高速摄像机(假定拍摄速度可以任意调高,即t的无限密集连续取值)拍摄到任意多张不同的状态照片,或者说当你看一段动态的录像的时候,你可以把它当作是无穷多张照片的集合。
统计物理学习惯把微观状态数和宏观状态的关系比喻为一张照片和一段录像的关系,这绝对是一个错误。状态,一定是某个时点上的“样子”,是一张“照片”,而“一段录像”是描述一个确定时长的事件过程。如果物理学果真将宏观状态看作是一段录像,那么就彻底混淆了过程函数和状态函数之间的区别了。
由于处于某种微观状态的粒子数是总数的一个部分,而总数是一次实验(一段录像)的结果(流量),因此,对应于某种速度状态的粒子数也是一个流量概念,而非存量概念。我们从一张照片上得不到一个微观状态数W的数据,也就是说,S=klnW和状态点不是一一对应的,即由S=klnW确定的S也不可能是一个状态函数,而只能是一个过程函数。
另一方面,统计熵的概念把熵和有序无序的概念挂起钩来,但是强调说有序就是不均匀,也并非整齐。这是毫无道理的。因为事实上存在着既均匀又有序也整齐的分布状态——例如把操场化分为均匀的方格,让个头相同男女各半的一群人男女间隔地站立在每个格子的中心,而且面向一致姿势统一。指挥员只需要说“各就各位!向前看!立正!”,就达到一个既均匀又有序又整齐的状态了。同样,在一块矿物结晶体当中也是均匀有序整齐的结构。
所以,不能够把“均匀”和“无序”等同起来。均匀,是空间分布的密度一致,而“序”和“整齐”的概念还涉及到“方向”和“速度”问题。
假如单纯用“均匀度”来表述“分布”,我们毫无疑问地确信,温度高的一团气体和温度低的一团气体在一个容器内的均匀度是丝毫不差的,都是100%均匀的。差异仅仅是在于达到均匀分布所需要的时间差异,即温度只是影响达到平衡态的时间长度。但是,平衡态的理念恰恰又是不考虑驰豫时间的——队伍可能是慢腾腾走到位置上的,也可能迅速入位,或者是有人动作迅速有人磨磨蹭蹭,但是最终还是会各就各位均匀分布。换句话说,均匀度和温度无关,或者说,由于热力学温度是指平衡态温度,而平衡态就是绝对均匀的状态,所以,温度高低只关乎达到平衡态的弛豫时间的长短,而和所谓的均匀度无关。也就是说,如果把统计熵看作是对某种分布的描述,则必然得出统计熵和温度无关的结论。这就和热温商与温度密切相关的概念完全不能融合了。
假如波熵S=klogW当中的W是描述微粒的空间位置和姿态的变化速度,我们倒是可以理解这个速度与温度有关,毕竟热锅上的蚂蚁比冷锅上的蚂蚁要“活泼”,但是,W不幸被界定为“均匀度”,这就和温度无关了——何以见得冷锅上爬的蚂蚁没有热锅上爬的蚂蚁分布的均匀?
在各种科学研究中,变化维度座标是经常的事情,我们可以把一个指数函数y=kex转化为一个线性函数Y=lny=x,把y-0-x坐标系当中的曲线转化为Y-O-x坐标系当中的一条直线。普朗克把玻尔兹曼对大数粒子速度分布的研究明晰化为S=klnw,其中k被称为波尔兹曼常数。但是在普朗克的表达中,取对数不过是几率的另一种计量方法而已,本质上应该是同一个东西。也就是说,如果W是一个可以成立的概念,则S=klnW不过是W的另一个表示方法,和所谓的熵概念毫无关系。
对数坐标,侧重于变量数量级的考虑。这就像化学中氢离子浓度[H+]和pH值之间的关系(pH=-log[H+])一样,pH=2表示的氢离子浓度是0.01数量级的,要比pH=1所表示的0.1级的[H+]低一个数量级。假如把所谓的微观状态数W加一个对数运算就可以形而上地称为“统计熵”的话,我们岂不是也可以把pH值叫做“酸度熵”或者“化学熵”了?甚至叫做“负酸熵”或者“负化学熵”了?同样,pOH也可以叫做“碱熵”或者“负碱熵”了?
我们从波尔兹曼统计熵概念对热力学第二定律的描述中——在孤立系统中,熵的增加对应于分子运动状态的几率趋向最大值(即最可几分布)——就不难看出,波尔兹曼的统计物理学理论和热力学的热温商理论一样,都是和现实世界不符合的。例如宇宙会自动从“宇宙汤”演变成为各种运动有序的星系;可以自行演化出我们这群试图偷窥其奥秘的智人;作为一个孤立系统,和宇宙大爆炸相反的过程(万物归一,塌陷回到奇点)也是自发的……在这些自组织的自发过程当中,状态数Ω显然应该被认为是减小的,那么按照S=klnΩ就有⊿S=kln(Ω2/Ω1)<0,是一个熵减过程。这就否认了孤立系统的自发变化一定是熵增的论断。
统计熵的概念可以独立成立,把“熵”同物系自身的“序”联系起来,理顺了前帖所说的“用两个事物之间的关系定义其中之一的内在性质”的矛盾。但是,如果再回过头来和热温商挂起钩来,等于前功尽弃。我们就可以看出前面提到的热温商理论当中关于基点熵S0可以任意取值的说法是毫无道理的——因为不存在一个可以任意取值的分布基态W0。
(请续看下帖——“三熵”对比之二)
 爱华网
爱华网