------纳什均衡、进化稳定策略与随机稳定状态
摘要:均衡思想贯穿于经济学的各个方面,非合作博弈理论与进化博弈理论也不例外。本文将系统地论述纳什均衡、进化稳定策略及随机稳定状态这三大均衡概念之间的内涵与处延,同时给出了不同均衡的算法,在此基础上分析它们之间在描述系统稳定性上的区别与联系。
关键词:纳什均衡;进化稳定策略;随机稳定状态
The evolution of equilibrium ideology in game
Abstract: Equilibrium ideology penetrates into every aspects of Economics not excepting the non-cooperative game theory and evolutionary game theory. The paper will systematically discuss the connotation and extension of three equilibrium concepts, which are Nash equilibrium, Evolutionary stable strategy and Stochastic stable state, presenting different formulas for accounting equilibrium. On the basis, the paper further analyzes their differences and relations while describing systematic stability.
Keywords: Nash equilibrium; evolutionary stable strategy; stochastic stable state
引言
在经济学领域均衡思想与演化思想一直处于不断的斗争中,均衡思想能够充分运用数学特别是最优化的数学工具,可以通过简单的计算得出预测结果,固有的缺陷就是它有如完全理性、完全信息等非常严格且与现实不太相符的假定,因而,由此所得到的许多结果缺乏解释力。演化思想并不要求理性假定,通过深入到参与人行为动机的背后中考察参与人的行为,运用动态过程来描述行为的演化,进而得出系统的最终结果。演化方法更贴近现实,由此得到的结论也就更有实际价值,能够较好预测参与人的行为。本文以非合作博弈理论的纳什均衡、进化博弈理论的进化稳定策略及随机稳定状态三大均衡概念为主线,系统地分析了各概念蕴涵的思想,并给出相应的算法,在此基础上运用例子及图像更直观地给出三大概念之间的区别与联系。
一、博弈均衡思想的演化
著名经济学家马歇尔早就说过,经济学有两大研究路径:一是沿着来源于经典牛顿力学的均衡思想;一是沿着来源于生态学的演化思想。纵观经济学的发展历史可以看出这两种思路一直在此起彼伏地斗争着。1890年马歇尔出版了标志着新古典经济学形成的《经济学原理》[1]一书后,均衡思想占据了统治地位,成为经济学家研究的主要方法。运用数学领域的“不动点定理”证明纳什均衡(Nash 1951)[2]的存在性,使得纳什成为第一个用不动点定理于经济学研究的经济学家,他因此获得了1994年的诺贝尔经济学奖;此后,经济学家德布鲁(Debru 1954)[3]应用“不动点定理”证明了一般均衡的存在而获得了1983年的诺贝尔经济学奖,他们的工作把均衡思想推向了高潮。物理学的中均衡就是不动,其前提条件就是:物理学中的变量多数是可以控制的,并且一般是与时间无关的。但运用均衡思想来研究在时间上不满足可逆性的社会人行为就显得有点牵强附会了,为了迎合均衡思想,经济学家给参与人附加如理性、完全信息等不切实际的假定,使得经济学离现实越来越远了,这正是理性框架下难以得到合理结论的一个主要原因。随着经典博弈理论、生态理论及心理学理论研究的深入发展,特别是心理学家西蒙把其在心理学领域研究的成果直接应用经济分析并因此获得了诺贝尔经济学奖,极大地激励着经济及社会学家从现实人行为出发来解释经济及社会现象,2002年诺贝尔经济学奖授予给丹尼尔·卡内曼标志着经济学的研究对象从传统的“经济人”转向现实的“社会人”,从现实社会人出发的演化经济学、进化博弈理论等获得了迅速发展,从均衡思想的演化来看,越来越多经济学家把注意力转向了进化稳定策略(Maynard Smith, J. and Price. G. R(1973))[4]与随机稳定状态(Foster and Young 1990)[5]等的研究、从短期均衡转向了长期稳定性研究,所用的均衡概念从纳什均衡到进化稳定均衡再到了随机稳定性,从理想化的世界慢慢地转向了现实世界。
二、纳什均衡、进化稳定策略及随机稳定状态的内涵
非合作博弈理论中最基本的均衡概念就是纳什均衡,它只能描述均衡点的局部静态性质;进化博弈理论基本均衡概念就是进化稳定策略,它是也是一个静态概念,但可以描述系统的局部动态性质;进化博弈理论另一个重要概念就是随机稳定状态,它是一个动态概念,能够描述系统的全局动态性质。与前两者不同,随机稳定状态并不是不动的,它只能描述系统的一种长期行为,从长期来看,系统在随机因素影响下绝大多数时间都处于某个均衡,下面分别阐述三个概念。
2.1 纳什均衡思想及其内涵
非合作博弈论研究面对利益冲突的个体互动时,参与人的策略反应。给定利益冲突每一个参与人必须从既定的选择集中作出选择。在博弈论中选择就是策略,选择集就是策略集。每一个参与对选择集中的各个策略都有既定的偏好,所有参与人的选择决定了博弈的结果。
博弈论关心的问题之一是:面对特定博弈,其解是什么?博弈论的最重要的解就是由博弈论理论家Nash(1951)在研究非合作博弈问题时提出来的纳什均衡。所谓纳什均衡策略是一个策略组合,是指在其他参与人选择一定的条件下,每一个参与人都选择获得最大支付的策略,换句话说,纳什均衡状态就是任何单独偏离不会得到改善的一种状态。下面给出纳什均衡的正式定义(张维迎《博弈论与信息经济学》1994,P69)[6]:
定义:有个参与人的战略表示式博弈,策略组合是一个纳什均衡,对每一个参与人,都是给定其他参与人选择时第个参与人的最优选择。
即。
其实在求解纳什均衡时,就是解联立的偏微分方程组。显然,纳什均衡是一个局部最优而非全局最优均衡概念,因此,纳什均衡并不能保证就是支付最高的不动点[1]。由此便引出了帕累托效率均衡:没有所有参与人都得到更高支付的其他选择的均衡就是帕累托效率均衡,用数学语言来描述(Menasché.D.S. et. al. (2005))[7] :
有个参与人的战略表示式博弈,策略组合是一个帕累托效率均衡,对每一个参与人,都不存在满足
(2)
博弈论关心的问题之二是:参与人是如何进行策略选择的,为什么会选择纳什均衡策略?非合作博弈理论假定参与人是完全理性的,在处理动态博弈时,还要求参与人满足序贯理性[2]这一比理性更强的要求。在如此强的假定下,参与人会对世界的任何变化都会作出最优反应,因此,如果存在均衡,那么参与人总会选择均衡策略,但在处理多重要均衡问题时,由于参与人难以推测对方的反应,因此,无法在多重均衡之间进行选择,尽管博弈论理论对此进行了广泛而深入的研究,但正如Ken Binmore在给Weibull(1995)[8]的“evolutionary game theory”一书作的序言中指出:“However different game theorists proposed so many different rationality definitions the available set of refinements of Nash equilibrium became embarrassingly large, Eventually almost any Nash equilibrium could be justified in terms of someone or other’s refinement”。有关纳什均衡算法可参阅王则柯,李杰(2005)[9]。
2.2 进化稳定策略思想及其内涵
进化稳定策略这一进化博弈理论的基本均衡概念是由生态学家Maynard Smith, J. and Price. G. R(1973)在研究生态现象演化时提出来的。原初定义(见张良桥2003)[10]有许多限制条件如对称博弈、孤立的随机冲击、参与人数目无限多等等。尽管许多理论家从不同的方面对此概念进行了拓展,但他们提出的原初概念却能够很好表达出进化稳定策略的含义。下面先给出Maynard Smith and Price(1973)的原初定义,然后,我们给出一种计算博弈进化稳定策略的方法。
2.2.1 进化稳定策略的定义
设是矩阵,由于是对称博弈,因此可以用第一个参与人的支付矩阵来描述整个博弈,其中表示策略者与策略者博弈时,策略者所得的支付。概率向量(也就是混合策略),其中。
(3)表示与选择混合策略者博弈时,选择策略者所得到的期望支付。为了说明的方便,下文称策略为稳定策略;策略为突变策略。
说策略是进化稳定的,如果满足:
并且,对,若有,那么就要满足:
条件(4)说明了进化稳定策略一定是纳什均衡策略,条件(5)说明弱纳什均衡策略必须要满足的附加条件。显然,在对称博弈中,严格纳什均衡策略一定是进化稳定策略。
直观含义:首先,我们可以看出所有进化策略都是纳什均衡策略,所进化稳定策略集是纳什均衡策略集的子集,非纳什均衡策略就不是进化稳定策略;其次,由定义中的两个条件可以得出,稳定策略者与稳定策略者群体博弈时,突变策略者不会比稳定策略者好;如果突变策略者与稳定策略者一样好,那么,突变者策略与突变策略群体博弈时,就没有稳定策略者与突变策略群体博弈时好。也就是说,稳定策略具有对少数突变者的免疫力,在稳定状态时,突变者是不容易侵入的。
2.2.2 进化稳定策略的算法
计算进化稳定策略的方法主要有两大类:一是从动态过程出发,求出系统的平衡点,然后,再根据进化稳定策略的定义进行验证就可以了;另一种方法就是直接用进化稳定策略定义来求。第一种方法涉及到具体的动态过程,并且只要知道动态过程就很容易求出进化稳定策略,本文略(可以参考张良桥2001)[11]。第二种方法就是通过定义来求,下面给出一种简单的处理方法。
根据纳什均衡的定义可以知道,如果策略是博弈的纳什均衡,那么,所有以正概率进入最优混合策略的纯策略都是最优的,参与人在所有这些纯策略所得的支付都是无差异的(见《博弈论与信息经济学》102-103页,张维迎),即有:
表示混合策略中非零概率的纯策略。假定存在且下标为的纯策略满足,令B是矩阵A中对应于非零纯策略的阶子矩阵。且令C为矩阵,其中代表元素为:。那么当且仅当C是负定的,就是进化稳定策略(见John Haigh 1974)[12]。
证明:假定,并且存在,有,那么很明显有,其中是第个纯策略,即在与稳定策略者群体博弈时,突变策略者得到的支付比稳定策略者还要大,所以策略不是进化稳定策略,所以式(6)是进化稳定策略的必要条件。因此,对应于非零概率的纯策略满足:,对满足条件的策略有(注意):
对任意,当且仅当
有:。综上所述,利用该方法来求进化稳定策略的步骤如下:
首先,令个非零混合策略,然后解个方程:,定义B,C再考察矩阵C的所有特征根是否都为负,若都是负则所得的策略就是进化稳定策略。
如求对称博弈,它有两个进化稳定策略:。
如果某策略组合是严格纳什均衡策略,那么就可以直接得出它就是进化稳定策略,但如果是弱纳什均衡策略,那么就可运用上述的方法来进行判定。由此,可得到求博弈的进化稳定策略步骤:一是求出博弈所有的纳什均衡;二是由支付判断出其中的严格纳什均衡;三对非严格纳什均衡而言就代入上述方程,并判断是否为负定即可以求出博弈中所有进化稳定策略。
2.3 随机稳定状态思想及其内涵
Maynard Smith, J. and Price. G. R(1973)提出的进化稳定策略概念要求突变因素不连续且不重叠,它只能描述在单个随机因素影响下任何偏离均衡状态的行为都会随着时间的演化自动回复到原来的进化稳定状态。现实中,经济系统常常会受到来自突变和其他偶然事件的冲击,这些因素可能会对系统产生不可忽略的影响,Foster and Young(1990)认为,首先,原初ESS概念把影响系统的因素都看成是一个个孤立的事件,假定一个因素的影响消失以后,再考虑另一个因素对系统的影响,而在现实中系统常常会受到连续的随机冲击。事实上,现实中出现上述情况纯属偶然现象,一个只能处理偶然现象的理论是没有任何存在价值,尽管单个随机因素对动态系统的影响较少,但它们却可能对系统产生累积作用而定量地改变系统的稳定性,使得系统离开进化稳定状态,系统什么时候回复到当初的进化稳定状态,依赖于动态过程的全局结构;其次,原初ESS定义是一个局部概念,因此在考虑随机冲击时就不能作为判断系统稳定性的标准;再次,由于系统的极限行为依赖于初始条件,同时在吸引子集合中只有一部分状态是随机稳定的,且随机稳定状态的选择还依赖于随机过程特定的结构,因此,ESS和没有充分地考虑到随机因素对进化系统影响的吸引子(Attractor)在描述随机系统的稳定性时都不理想。
2.3.1 随机稳定状态的定义
一般的进化模型中参与人都是选择那些相对于群体分布的最优反应策略,群体分布随着时间的演化而为不断变化的,这是一种奈特不确定性,并且在这种动态下,系统一定会收敛到协调博弈的严格纳什均衡,偶尔也可能出现极限环的情况,运用进化稳定策略概念依然无法在严格纳什均衡之间作出选择。Young(1990)首次把影响系统的随机因素纳入到进化模型之中并提出了既不同于传统ESS也不同于吸引子(Attractor)的随机稳定性(Stochastic Stability)概念,把均衡选择问题转变成不同均衡的吸引域宽度比较问题,有最宽吸引域的均衡就是随机稳定状态。随机稳定状态的定义如下:
定义:群体向量是随机稳定的,如果随着随机影响,极限密度对的每一个小邻域都赋有正概率;更准确地说: 其中。其中是当时,的极限分布,表示随机因素对系统所产生的影响。
粗略地说,一个状态P是一个随机稳定的,如果在长期中,随着随机冲击因素影响的不断变少,系统几乎一定(nearly certain)不会离开P的任意少的邻域。随机稳定的群体向量总是存在的,它有如下性质:随着及,它是一个最小闭集。根据上述定义,随机稳定状态与系统所定义的动态有关,如果是支付单调动态并且有不变突变率,随机稳定状态直接由吸引域的宽度确定(参阅Young(1993)[13]; Michihiro Kandori, Greorge J,. Mailath, Rafael Rob (KMR)1993[14]; Glenn Ellison2000)[15]。
2.3.2 随机稳定状态的算法
从定义可以看出,随机稳定状态是描述系统长期行为且由概率来定义的。如果系统是连续情形,那么可根据Foster and Young(1990)通过求系统随机潜力的方法来求随机稳定状态,即有最小随机潜力的状态就是随机稳定状态。而现实中,多数情况都是离散的,下面将根据Freidlin, M. I and Wentzell, A . D. (1984)[16]的方法来给出有多个常返状态情形下随机潜力的计算方法。该方法首先要求每个参与人在任何状态任何时候都以相同且不为零的突变率选择其他任何策略,这样就可以保证系统的遍历性,从而存在平稳分布。假定系统有五个状态,并且每两个状态之间的阻抗(左图中箭头上的数字表示从一个状态到另一个状态的阻抗,右图是根据左图计算出来的):
状态之间没有标明数字就说明阻抗是无限大(其中的阻抗是根据突变率的指数来确定的),由上右表可以求出转移概率(因为我们只是为了求各个常返状态的阻抗,没有写出转移概率)。显然:该系统有四个常返状态。,,,,则不同常返状态之间的最小阻抗为(实际已经找到了常返状态之间的最短路径):
四个常返状态对应的随机潜力分别为1 5 3 6。因此,该动态系统的随机稳定状态就是具有最小随机潜力的状态即为。本例中直接给出各箭头旁边的数字,其目的是为了使问题简化,实际上它表示从一个状态到另一个状态的阻抗,在解决实际问题时,需要具体分析;另外,此例没有深入到突变产生的过程中去,突变率的不同系统的随机稳定状态就不同。
三、纳什均衡、进化稳定策略及随机稳定状态的比较
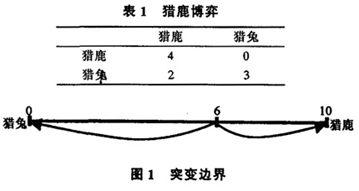
国内经济学界对纳什均衡及进化稳定策略这两个概念已经有了相当的了解,但很少有学者弄清随机稳定状态的内涵,下面将通过一个例子来综合说明这三大概念之间的区别与联系。在非合作博弈理论中,理性人是不会选择严格劣策略的,作均衡分析时常常剔除劣策略的。但是,在进化博弈理论中求随机稳定状态时,参与人尽管不会选择劣策略,但严格劣策略却可以影响其他均衡吸引域宽度,进而影响到系统的随机稳定状态,因而不可以剔除劣策略。下面例子既可以说明劣策略对随机稳定状态的影响,又可以说明纳什均衡、进化稳定策略及随机稳定状态之间的关系。
首先看左边的对称协调博弈,该博弈有两个严格纳什均衡与一个混合策略纳什均衡,其中两个严格纯策略纳什均衡是进化稳定策略;纯策略纳什均衡是系统的随机稳定状态[3]。现在加入第三个策略(如支付矩阵图3右),根据Ellison(2000))提供基于不变突变率的方法来计算可得:时它就是严格劣于第一个策略。
根据Ellison2000,当[4]时就可得到状态是随机稳定状态,即满足:
以上计算表明,只要支付,那么状态就是随机稳定状态。尽管严格劣策略不会成为均衡策略,便它却可以影响参与人的选择,通过改变常返状态吸引域宽度而改变长期均衡状态。在现实中,所谓的迂回战役、曲线救国、旁敲侧击、游击战等都属于这种情况,因为正面方法无法使得博弈均衡发生改变,只有通过其他的非正面方法来使得系统常返状态的吸引域发生变化,进而改变博弈随机稳定状态。
另外当,该博弈有两个纯策略纳什均衡,及一个混合策略纳什均衡;但由进化稳定策略的定义可知,该博弈只有两个进化稳定策略即两个严格纳什均衡(见Jörgen W. Weibull(1995)),混合策略是不稳定的鞍点均衡,因而不是进化稳定策略。显然,进化稳定策略是比纳什均衡策略更精炼的均衡概念;由上面计算可知,该系统只有状态是随机稳定状态,这样就再次去掉了吸引域较窄的其他均衡状态,因此,随机稳定状态是一个比进化稳定状态更精炼的概念。
下面用图5直观地说明它们之间的区别与联系。纳什均衡是指在其他参与人选择不变的条件下,每个人都选择了最大化自己期望支付的策略组合,纳什均衡点就是不动点,从图中可以看出其中的A、B、C、D四个点都是不动的,即都是纳什均衡点;进化稳定策略则是指对任何小的冲击都保持稳健性的一种状态,它不仅要求是纳什均衡而且还要求对外界一次性、不连续且孤立的冲击保持稳健性,它是一种邻域概念,要求系统在一定范围内保持相对稳定性,这样就排除了图中A、C两个鞍点纳什均衡;随机稳定状态则是指对任意随机冲击保持某种稳健性,从长期来看,系统花费大部分时间在某一状态,也就是随着随机冲击的不断减少,系统在该状态出现的概率几乎为1,它不仅是一个邻域概念而且还考虑到了吸引域的宽度,即有最宽吸引域的均衡才是长期随机稳定状态,图中只有D点表示的均衡才是随机稳定状态。从均衡的时间上来看,纳什均衡是一种短期均衡,进化稳定策略则是中长期概念,随机稳定状态则是一种长期均衡概念。
结束语
本文系统地论述了非合作博弈理论的纳什均衡概念、进化博弈理论中的进化稳定策略与随机稳定状态三个基本概念。当然,非合作博弈理论与进化博弈理论还存在许多其他的均衡概念,本文并没有给出相应的定义。另外本文只给出了不变突变率情形下系统随机稳定状态的算法,然而,现实中突变率并不满足此不变条件,所以需要进一步研究。
参考文献
[1] 阿弗里德·马歇尔[英],朱志泰译,《经济学原理》,第八版,华夏出版社,2005年1月.
[2] Nash, Jr. John F.(1951), Noncooperative games, Annals Mathematics 54.
[3]Arrow, K. and Debreu, Existence of equilibrium for a competitive economy, Econometrica, 1954,22, 265-290.
[4] Maynard Smith, J. And Price, B. R. (1973): The Logic of Animal Conflict, Nature, 246, 15-18.
[5] Young, P. and Foster, D. (1990): Stochstic evolutionary game dynamics. Journal of theoretical biology. 38, 219-232.
[6] 张维迎(2000):《博弈论与信息经济学》,上海人民出版社,第一版.
[7] Menasché.D.S. et et.al. (2005): An evolutionary game-theoretic approach to congestion control. Performance evaluation. 62, 295-312.
[8] Weibull, J. (1995): Evolution game theory. MIT, Cambridge, MassachusettsLondon, England.
[9] 王则柯,李杰(著)(2004):《博弈论教程》,中国人民大学出版社.
[10] 张良桥(2003):《论进化稳定策略》,《经济评论》,5;
[11] 张良桥(2001):《进化稳定均衡与纳什均衡:兼谈进化博弈理论的发展》,《经济科学》,3,103-111;
[12] John haigh(1974): Symposium on mathematical genetics, Mathematics Division, University of Sussex.
[13] Young, H. P. (1993): The Evolution of Conventions, Econometrica, 61, 57-84.
[14] Kandori, M., Mailath, G. J., and rob, R. (1993): Learning, mutation, and long-run equilibria in games, Econometrica, 61, 29-56.
[15] Ellison, G. (2000): Basins of attraction, long-run stochastic stability, and the speed of step-by-step evolution. Review of economic studies. 67, 17-45.
[16] Freidlin, M. I and Wentzell, A . D. (1984): Random perturbations of dynamical systems, Springer-verlag, Berlin/New York.
[1] 如显示集体理性与个体理性矛盾的囚徒困境博弈。
[2] 举一个例子来说明,两个人下棋,首先要求理性是共同知识,也就是双方都知道对方是理性的(因为博弈中只要一方不满足理性要求,那么博弈就无法分析下去),在此条件下,假如你下第一脚棋,你就应该想到下一步对方的反应,对方也知道你会想他反应,你又知道对方知道你会想到他的反应,如此下去……。
[3] 该均衡既是风险占优又是帕累托占优,所以一定是随机稳定状态(详细见Peyton Young(1993))。
[4] 表示进入状态的阻抗大于离开状态的阻抗。
 爱华网
爱华网


