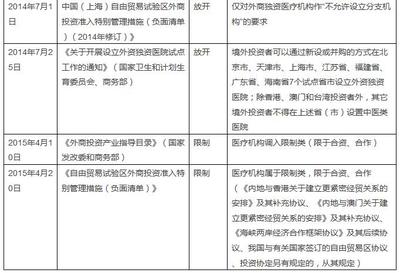
有这样一道关于5个海盗如何分赃的问题,说是5个海盗抢到了100颗宝石,每一颗都有一样的大小和一样贵重的价值,经过商议,他们决定将宝石这样分配: a、抽签决定自己的号码1,2,3,4,5。 b、首先,由1号提出分配方案,然后5人进行表决,当且仅当超过半数的人同意时,就按照1号的提案进行分配,否则,他将被扔入大海喂鲨鱼。 假设每个海盗都是很聪明的人,都能很理智地判断得失,从而做出选择,问题就是1号海盗应该提出怎样的分配方案才能够使自己的收益最大化? 根据题意,有如下分析: 由于5个海盗都是很理智的人,所以1号海盗首先必须要“保全自己的性命”,才能够实现自身利益的最大化,这是既是解决这一问题的前提,也是一个约束条件。因此,按照题意,他必须在剩下的4个海盗中争取至少2个海盗对提案的支持才能满足这个条件,而理性的1号海盗显然只需要争取2个海盗的支持就足够了。如何得到其中2个海盗的支持呢?这又必须满足两个条件: a、这2个海盗分配到的宝石数量相同。 b、这2个海盗手中的宝石数量不应少于(甚至会多于)1号海盗手中宝石的数量。 设1号海盗手中的宝石数量为X,1号海盗所争取的两个海盗手中的宝石数量均为Y,则有题意可知,1号海盗不需要争取的两个海盗手中的宝石数量完全可以为零(因为加上他自己,一共有3个人支持分配方案,其目的已经达到)! 因而,将问题转化为数学语言来描述,就是: 在 X≤Y的条件下,求满足关系式X+2Y=100时X的最大值。采用求解线性规划的方法,可求得最优解为X=32,Y=34。所以,为了在既定的约束条件下实现自身利益的最大化,1号海盗所提出的分配方案应该是:(32,34,34,0,0) 以上就是采用博弈论分析解决问题的一个案例。博弈论是研究竞争的逻辑和规律的数学分支,冯8226;诺依曼和摩根斯特恩合著的《博弈论和经济行为》一书是这门科学的奠基之作,不过他们所建立的是关于纯粹竞争的理论。纳什进一步证明了,在这一类的竞争中,在很广泛的条件下是有稳定解存在的,只要别人的行为确定下来,竞争者就可以有最佳的策略,这种状态即为所谓的“纳什均衡”。他的这项理论工作使得博弈论从此成为经济学家用来分析各种经济现象的有力工具。 “纳什均衡”首先对亚当8226;斯密的“看不见的手”原理提出了挑战。按照斯密的理论,在市场经济中,每一个人都从利己的目的出发,而最终全社会达到利他的效果。从“纳什均衡”引出一个悖论:从利己目的出发,结果损人不利己。5个海盗的命运就是如此。从这个意义上说,“纳什均衡”提出的悖论实际上动摇了西方经济学的基石。所以“纳什均衡”是对冯8226;诺依曼和摩根斯特恩的合作博弈理论的重大发展,甚至可以说是一场革命。

 爱华网
爱华网