在实际的大规模电力系统中,低频振荡问题已成为了限制跨区电网功率交换的较常见且危害较大的因素之一。国内外不少专家学者对电力系统低频振荡进行了大量研究,特征值分析法是其中的一种经典方法,它在工作点附近将系统进行线性化,形成系统状态方程矩阵,进而求取特征值,但其计算数学模型的阶数不能过高,不能很好地考虑各种非线性因素,难以适应大规模电网在线分析的需要[2,3],而且在实际应用中却很难精确确定大规模电力系统的模型参数。基于Prony分析法的低频振荡研究可对时域仿真结果或实时测量数据提取振荡特征,适合于大规模线性动态系统的辨识],该方法对噪声较敏感,较难选取模型阶数,不能直接完成多输入多输出系统辨识。子空间方法[8]基于输入输出数据构建系统状态相量,在此基础上求解最小二乘问题得到系统的传递函数矩阵,最后求解此传递函数矩阵,获得表征系统动态特性的各量,数值稳定性好、无须优化过程,计算速度快,子空间模型辨识(SMI, subspace model ident-ification)方法自从20世纪90年代初提出以来就获得了广泛的关注[9],成为一种确定多输入多输出(MIMO)系统模型的有效方法之一。 到目前为止,SMI算法已成功应用于市政、机械工程等领域,文献针对建立有明确物理含义的发动机模型要求,首次提出并推导了指定状态变量的子空间辨识方法。子空间法应用于电力系统低频振荡辨识时,一般难以测得输入或激励,而随机子空间法(Stochastic Subspace Identification,SSI)则很好地解决了这个问题,随机子空间法是近年来发展起来的一种线性系统辩识方法,可以有效地从环境激励的结构响应中获取模态参数,其核心是把“将来”输出的行空间投影到“过去”输出的行空间上,投影的结果保留了“过去”的全部信息,并用此预测“未来”,它直接作用于时域数据,避免了计算协方差矩阵,采用矩阵的QR分解、奇异值分解(SVD)以及最小二乘等来识别离散后的系统状态空间矩阵,得到系统的动力学特性参数,辨识精度较高。下面本文从随机状态空间模型开始,逐步介绍SSI的基本思想,基本算法及其发展改进,最后阐述了SSI理论方面有待进一步研究的问题。 1. 随机子空间算法简介 子空间方法综合了系统理论、线性代数和统计学三方面的思想,直接由输入输出数据辨识线性时不变(LTI)系统状态空间模型,不需要参数化和迭代化,只通过一些简单可靠的QR分解、SVD分解等线性代数工具来实现,可直接估计状态空间模型,适用于多变量系统辨识,随机子空间法的基本原理则是将“将来”数据向“过去”数据进行垂直投影,进而根据该投影计算出可观测矩阵和一个卡尔曼滤波状态序列。 1.1随机状态空间模型描述 线性的离散状态空间方程:
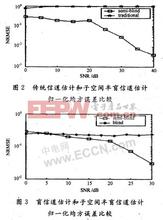
X(k+1)=Ax(k)+w(k) Y(x)=Cx(k)+v(k) (2.1) 图1为1号发电机功角振荡曲线,由以上分析可知,随机子空间分析直接作用于该输出信号,提取的振荡模式参数与电力系统分析综合程序(PSASP)的小干扰稳定程序模块分析结果基本一致。 3.应用及发展 SSI在系统正常运行或者小扰动下可直接识别弱阻尼模式、频率、阻尼和振型等模态参数。由于风力发电机组没有功角,采用数学模型方法分析含风电场的电力系统的低频振荡可能会产生一定的误差,文献提出基于实测信号的随机子空间算法对大规模双馈风机并网后的系统阻尼特性进行了分析。在系统处于异常运行或者故障状态时,文献直接根据端部量测数据识别出系统的低频振荡模态参数,运用EMD对量测数据进行时空滤波和平稳化处理,由SSI辨识出相应的系统状态矩阵,最终得到系统低频振荡模式参数。文献通过采集定子电流信号,将随机子空间法用于同步发电机参数辨识,基于数据驱动随机子空间辨识方法是通过小波技术消去信号中的噪声分量,然后消去直流分量,利用卡尔曼滤波估计得到系统的随机状态模型,提高了模式参数辨识精度,但卡尔曼滤波滤波状态序列又与过去输出有直接的关系,文献采用一个测点的信号作为“过去”作为输出信号代替全部测点的信号,减少了计算量,对随机子空间方法进行了改进。在随机子空间识别方法中,确定系统的阶数是该方法的关键工作,随机子空间方法确定系统阶次是通过考虑投影矩阵的奇异值分解所得的奇异值确定的,操作较困难,故实际应用中常采用稳定图方法确定阶次,文献用模态置信因子来消除虚假模态。为了方便快速地得到系统的模式及其对应模态,文献还引入参考通道技术,在不影响识别准确度的情况下极大地提升了计算效率,形成了一种改进的随机子空间方法,同时引入稳定图的思路,设计稳定图自动识别算法,实现了快速有效地辨别真伪模式。 介绍了随机子空间辨识方法,用该方法分别对测试数据和仿真数据进行模态参数识别,并与Prony分析结果相比,吻合较好,可以得到较好的辨识结果,但应用于线性系统动态模型的辨识时,该方法在模型阶次和系统阶次的选取上以及计算效率上还存在一些需要解决的关键问题,虽然这个阶数可在辨识过程中估计得出,由于一般环境激励采样时间较长,所得的数据数量非常庞大,所需时间长,而采用稳定图方法确定阶次容易识别出虚假模态。
 爱华网
爱华网