分数布朗运动下的Black-Scholes公式及其推广
唐斌,陈柳钦*
(南开大学深圳金融工程学院,深圳,518055)(天津社会科学院,天津,300191)
[内容摘要] Ciprian Necula 利用分形几何等知识推导出分数布朗运动下的Black-Scholes期权公式,但这篇论文推导过程比较复杂,对于布朗运动是分数布朗运动在当H=时的一个特例也没有很好地予以阐述。本文在此基础之上,用一种简单易懂的方法对他的公式重新进行了推导证明,并对这一公式与传统的Black-Scholes期权公式进行比较分析,从而论证了布朗运动只是分数布朗运动的一种特例。最后,将这一公式推广到看涨-看跌期权平价公式和有红利支付的股票期权定价分析之中。
[关键词]分数布朗运动;热传导方程;有效市场假设;分形市场假设;Black-Scholes期权公式
[中图分类号]:F830
1、引言
自从Black-Scholes期权公式 被提出之后,这一公式便被广泛地应用于金融市场的定价分析,但是由于这一传统的Black-Scholes期权公式是建立在有效市场假设之上,认为金融资产的价格波动是相互独立的,即服从布朗运动,而其收益率则是呈现独立同分布的随机变量,并服从正态分布。但近年来,对股票市场的大量研究结果都表明股票市场价格变化并不符合正态分布,它们呈现的是一种“尖峰胖尾”分布,而且股价之间也不是随机游走的,而是不同时间存在着长期相关性。1994年,Peters提出了分形市场假说,它强调信息和投资起点对投资者行为的影响,并应用R/S 分析法证明了不同资本市场都存在着分形结构和非周期循环。分形市场假说由于不依赖于独立及正态分布等假设,利用分数布朗运动能够很好地解释酱市场中的“尖峰胖尾”现象。因此必须对传统的Black-Scholes期权公式进行修改,推导出分数布朗运动下的Black-Scholes期权公式。
Ciprian Necula用傅立叶变换方法,推导出了分数布朗运动下的Black-Scholes期权公式。但由于他在推导时应用了许多分形几何等数学知识,使得有关这一模型的证明过程不易于被一般人所理解。而且他的这篇论文对于布朗运动是分数布朗运动在H=时的一个特例也没有很好地予以阐述。为了弥补他这文章的不足之处,使这一模型更易于理解,本文在他的这篇论文基础之上,用一种简单易懂的方法对分数布朗运动下的Black-Scholes期权公式重新进行了推导证明,并将其与传统的Black-Scholes期权公式进行比较分析,从而论证了布朗运动只是分数布朗运动的一种特例。最后,将这一公式推广到看涨-看跌期权平价公式和有红利支付的股票期权定价分析之中。
2、分数布朗运动介绍
分数布朗运动具有如下几个性质:
(1)Hurst参数为H(0<H<1)的分数布朗运动是一个连续的Gaussian过程:
(2)当H>时,具有长期依赖性,
即:,且有
①若H=,即为标准布朗运动B(t),表现为随机游走特性。
②若0<H<,具有反持久性,即过去的增量与现在的增量呈负相关关系,H距离0越近,这种反持久性行为的强度越大。
③若<H<1,具有持久性,即过去的增量与现在的增量呈正相关关系,随H逐步逼近1,其持久性趋势越强。
(3)自相似性。
3、无风险套利组合的构造
为了构造出一个无风险套利资产组合,首先假设:
(1)标的资产的价格运动满足:
当,
可得:,从而有S(t)服从几何分数布朗运动;
(2)无风险利率r是常数;
(3)原生资产不支付股利;
(4)不存在交易成本和税收等影响因素,且无套利机会存在。
在<H<1和风险中性的假设条件之下,利用D-对冲,推导出分数布朗运动下的期权价格的偏微分方程。建立一个资产组合:,其中D为原生资产的份额,选取适当的D使得在(t,t+dt)时段内,这一资产组合是无风险的。Hu and Oksendal (2000)已经证明不存在无风险套利。
又因为有
且有
由以上两式可得:
又因为和
从而得到分数布朗运动下的偏微分方程[①]如下:
4、分数布朗运动下Black-Scholes公式的推导
在得到分数布朗运动下的偏微分方程之后,我们利用函数变换,将偏微分方程化成Cauchy问题,再利用Possion公式便可以推导出分数布朗运动下的Black-Scholes期权公式。
4.1 公式的证明
具体证明过程如下:
其中:
.
证明:
在(5)式的PDE方程中,对其做如下变换:
令 x=㏑S,
则有
代入PDE方程得到:
令
从而有:
利用Poisson公式,解此Cauchy问题,其解为:
同时令:
将X代回原变换值,即得:,从而得证。
4.2 与传统的Black-Scholes期权公式的比较
通过比较两个期权公式,可以发现布朗运动是分数布朗运动在H=时的一个特例。当H=时,分数布朗运动下的Black-Scholes期权公式与传统的Black-Scholes期权公式是一致的:
但是,分数布朗运动又比传统的Black-Scholes期权公式更能解释资本市场中的价格变化现象。在传统的Black-Scholes期权公式中,期权价格只与股票价格S有关,而与T,t无关,但实际情况是期权价格既与股票价格有关,也与T、t有关。而在分数布朗运动中,期权的价值不仅与股价S,T和t有关,而且由于股票价格的变化具有长相关性,因此期权的价值还与Hurst系数H有关。假如有两个到期日T相同,而发行日不同的看涨期权,一个发行日为t1,另一个发行日为t2,其中t1<t2,并且假定两者的Hurst系数值H不相同。此时,若按照传统的Black-Scholes期权公式,可以求得它们在同一个时刻点t(t1<t2<t<T),将具有相同的期权价值,但是由于Hurst系数H的不同,使得它们在分数布朗运动下的期权价值不一样(只有当H=时两个期权的价值才会相等)。
另一方面,我们若将两个公式对应的希腊字母进行比较,可以发现在H=时,传统的Black-Scholes期权公式得到的希腊字母与分数布朗运动下的Black-Scholes期权公式得到的希腊字母又是一致的,各个希腊字母的表达式分别是:
(1)Delta——期权价格与股票价格的变化情况:
分数布朗运动下的,
当H=时, 它与用传统期权公式得到的是一致的。
(2)Gamma——衡量Delta变化的速度:
在分数布朗运动中
当H=时, 它与用传统期权公式得到的是一致的。
(3)Theta——期权时间价值的折损的速度:
分数布朗运动下的 ,
当H=时, 它与用传统期权公式得到的 是一致的。
(4)Vega——期权价格对股票价格波动率的敏感性:
分数布朗运动下的,
当H=时, 它与用传统期权公式得到的是一致的。
(5)Rho——无风险利率的变动的变动对于期权价格的影响程度:
分数布朗运动下的,
当H=时, 它与用传统期权公式得到的是一致的。
5、公式的推广
5.1 看涨-看跌期权的平价关系
设c(S,t),p(S,t)分别为具有相同执行价格K和到期时T的欧式看涨与看跌期权的价格,其中无风险利率为r,,红利支付率为d,则看涨-看跌平价公式为:
证明:
因为看涨期权与看跌期权存在如下关系:
所以,W(S,t)必然会满足以下关系:
设 ,将其代入上式,得到
又有
代入求解,即可得看涨-看跌平价关系:
5.2有红利支付时的股票期权定价
当对有红利支付的股票期权进行定价时,假设红利支付率为d:利用D_对冲,可以构造一个这样的投资组合:
其中股票价格的变动满足:
在风险中性假设之下,u= r(r为无风险利率)
利用本文介绍的推导方法可以得出:
,
其中:
6、 结论
本文通过对分数布朗运动下的Black-Scholes期权公式的证明,并将其与传统的Black-Scholes期权公式进行比较,论证了布朗运动只是分数布朗运动在H=的一个特例,然后在此基础上,将这一公式推广应用于看涨-看跌期权平价公式和有红利支付的股票期权定价分析之中。本文论证的分数布朗运动下的Black-Scholes期权公式可以应用于当前的金融市场定价问题之中,它克服了传统的Black-Scholes期权公式的一些不足之处,能很好地解释金融资产的价格变动现象。因此,它将会比传统的Black-Scholes期权公式具有更大的实用价值。
参考文献
[1]Bayraktar, E., Poor, H. V. and Sircar, R. (2004). Estimating the fractal dimension of the S&P 500 index using wavelet analysis, Intl. J. Theoretical and Applied Finance 7: 1–29.
[2]Cutland, N. J., Kopp, P. E. and Willinger, W. (1995). Stock price returns and the Joseph effect: A fractional version of the Black-Scholes model, Progress in Probability 36: 327–351.
[3]Greene, M. T. and Fielitz, B. D. (1977). Long-term dependence in common stock returns,Journal of Financial Economics 4: 339–349.
[4]Hu, Y. and Øksendal, B. (2003). Fractional white noise and applications to finance,Infinite Dimensional Analysis, Quantum Probability and Related Topics 6: 1–32.
[5]Maheswaran, S. and Sims, C. A. (1992). Empirical implications of arbitrage free markets,In Models, Methods, and Applications of Econometrics edited by PCB Philips .
[6]Willinger, W., Taqqu, M. S. and Teverovsky, V. (1999). Stock market prices and longrange dependence, Finance and Stochastics 3: 1–13.
[7]Ciprian Necula,Option pricing in a Fractional Brownian Motion Enviroment, Preprint, Academy of Economic Studies Bucharest, Romania, www.dofin.ase.ro。.
[8]Duncan,T.E.,Y.HuandB.Pasik-Duncan,Stochastic calculus for fractional Brownian motion,I.Theory,SIAMJ.Control Optim.38(2000),582-612
[9] (美)约翰·马歇尔,维普尔·班赛尔著,宋逢明等译:《金融工程》[M],清华大学出版社,1998年版。
[10]基思·卡思伯森, 德克·尼奇著,张陶伟, 彭永江译:《金融工程:衍生品与风险管理》[M],中国人民大学出版社,2004年版。
[11]宋逢明:《金融工程原理:无套利均衡分析》[M],清华大学出版社,1999年版。
[①] 传统的Black-Scholes的PDE为: (即H=)对两式进行比较可以看出,分数布朗运动是用代替传统的Black-Scholes下偏微分方程的s。
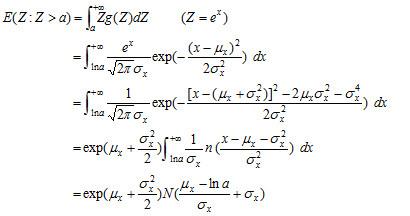
 爱华网
爱华网