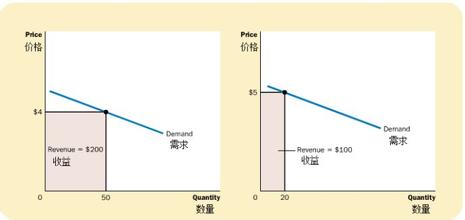
〖内容提要〗 需求价格弹性是经济学上衡量价格变动与需求量变动关系的一个指标,指的是需求量的变动对价格变动反应的敏感程度,那么商品的价格与销量的乘积即总收益的变动就可以最终归结为两个因素:价格变动幅度与需求价格弹性的大小,而且这两个因素也会影响总收益与总成本之差即总盈利。本文在修正需求价格弹性与总收益关系的基础上,确定了使企业总收益增加的合理调价范围和获得最大收益的最优调价幅度,并制定了企业取得最大盈利的最优价格,为企业的价格决策提供有利的参考。〖关键词〗需求价格弹性 阈值 最优调价幅度 最优价格一、需求价格弹性(Ed)及其相关原理的表述 1、需求价格弹性的概念及类型需求价格弹性是经济学上衡量价格变动与需求量变动关系的一个指标,用来表示在一定时期内某种商品的需求量的相对变动对其价格变动的反应程度,是商品需求量的变动率与价格的变动率之比。即: 需求价格弹性系数= 若以P、Q分别表示初始价格和需求量 ,以P1、Q1表示变动后的价格和需求量,以ΔP、ΔQ分别表示价格和需求量的变动量,以Ed表示需求价格弹性系数。则需求价格弹性的公式为: Ed= = 这里需要指出的是,根据需求规律,在其他条件不变的前提下,商品的价格变动与需求量变动是呈负相关的,因此Ed是一个负值。 通常以需求价格弹性系数绝对值的大小将其分成五种 :若 >1,被称为需求富有价格弹性,它表示需求量的变动率大于价格的变动率;若 <1,被称为需求缺乏价格弹性,它表示需求量的变动率小于价格的变动率;若 =1,需求呈单一价格弹性,它表示需求量的变动率与价格的变动率相同;若 =0,需求无弹性,它表示价格无论怎样变动都不会引起需求量的变动;若 = ,需求具有完全弹性,它表示价格微小的变动会引起需求量巨大的变动,即在既定价格下需求量可无限增加。 2、需求价格弹性系数Ed的测算 由于在实际经营活动中企业所面临的需求曲线是难以拟合的,所以通常所谈到的Ed是通过对资料的调查、收集、整理、分析,按照起点基数法确定特定价格P和特定需求量下的需求价格弧弹性。 3、需求价格弹性与总收益之间关系的一般表述 价格变动会引起需求量的反方向变动,而所引起的总收益变动就可最终归结为价格变动幅度与需求价格弹性两个因素的影响。在诸多西方经济学或管理经济学教材中,大致都这样表述:表1 需求价格弹性与总收益之间关系的一般表述 >1 =1 <1 =0 = 降价 增加 不变 减少 同比例价格的下降而减少 既定价格下,收益可以无限增加,因此厂商不会降价涨价 减少 不变 增加 同比例价格的增加而提高 收益会减少为零二、需求价格弹性在以总收益最大为目标的价格决策中的应用 1、对需求价格弹性与总收益之间关系的修正 当然我们从直观上想象,若 >1,当价格下降时,需求量增加的幅度比价格下降的幅度要大,显然总收益是增加的。但事实果真如此吗?不妨举个例子来讨论一下。 假设荔枝每千克10元时市场需求量为100千克,经调查分析,需求价格弹性为-2,此时总收益为1000元。根据表1的结论,水果商降价会带来收益的增加。当价格降至每千克8元即价格下降20%,那么需求量将增加40%增至140千克,此时总收益为1120元,降价会带来总收益的增加;当价格降至每千克4元即价格下降60%,那么需求量将增加120%增至220千克,此时总收益为880元,降价反而会使带来总收益减少。可见,表1的结论并不完全准确,当 >1时,要使总收益增加,价格下调的幅度应有所限制,那么阈值究竟是多少呢? 首先讨论两个极端情况,当 =0和 = 时,价格变动和需求量变动在数值上没多大联系,调价幅度对表1的结论没有影响。接下来主要分析 >1、 <1、 =1三种情况。 若用Δπ表示收益的实际变动额, P、Q为价格变动前的价格和需求量,ΔP、ΔQ分别表示价格变动额和由价格变动引起的需求量的变动额,结合(1)式,则:Δπ=(P+ΔP)( Q+ΔQ)- PQ = PQ (1+ )(1+ )- PQ = PQ( + + )=PQ (1+Ed+ Ed)调价后要使收益增加,即要求Δπ>0,分调高和调低价格两种情况讨论: 1) 若调低价格即 <0,要使Δπ>0,则须使(1+Ed+ Ed) <0,即 <-1- Ed,因为Ed<0,则要求 > -1。 当 >1时, -1<0,如果 ( -1,0)时,Δπ>0。也就是说,当商品的需求富有弹性时,价格下降幅度在( -1,0)内,总收益会增加;降价幅度为 -1时,总收益不变;而降幅超过( -1)时,总收益反而会减少。当 1 时, -1 0,则 > -1 0,显然与调低价格 <0相矛盾。也就是说,当 1时,降价不可能使总收益增加。见如下分析:若 <0,要使得Δπ<0,则要求(1+Ed+ Ed) >0,即 < -1,而该条件在 1时恒成立。可见当 1时,只要是降价,总收益必定会减少。 2) 若调高价格即 >0,要使Δπ>0,则须使(1+Ed+ Ed) >0,即 要求 < -1。分 <1、 1两种情况讨论,分析与调低价格时类似,在此就不赘述了,只给出最后结论: 当 <1时,价格下降幅度在(0, -1)内,总收益会增加;涨价幅度为 -1时,总收益不变;而涨幅超过( -1)时,总收益反而会减少。当 1时,只要是涨价,总收益必定会减少。 综上所述,我们可将需求价格弹性与总收益之间的关系修正如下表:表2 需求价格弹性与总收益之间关系的修正 >1 =1 <1 =0 = 降 价 降幅在( -1,0)内,收益增加;降幅为( -1)时收益不变;而降幅超过( -1)时收益减少 减少 减少 同比例价格的下降而减少 既定价格下,收益可以无限增加,因此厂商不会降价涨 价 减少 减少 涨幅在( -1,0)内,收益增加;涨幅为( -1)时收益不变;而涨幅超过( -1)时收益减少 同比例价格的增加而提高 收益会减少为零 可见,对于不同的需求价格弹性,价格升降能否为企业带来更大的收益,在价格的升降不超过阈值( -1)范围内存在一种必然的联系;但升降幅一旦溢出阈值,那种弹性与收益的必然联系就不复存在,那么企业通过价格决策改变收益状况时,要注意调价幅度不可溢出阈值。同时还可以看到,当 =1时,无论是降价还是涨价都会使收益减少 ,因此企业把价格定在单位弹性点上即企业在单位弹性点上组织生产,其收益将达到最大。 2、选择最优的调价幅度使企业总收益达到最大 既然企业定价在单位弹性点上时总收益达到最大,那么企业怎样调整价格才能使企业在单位弹性点上组织生产呢? 总收益TR=PQ[1+(1+Ed) + Ed]TR对调价幅度 求一阶导数,TRˊ=PQ(1+Ed+2Ed ),要使TR最大,则要求TRˊ=PQ(1+Ed+2Ed )=0,即 =- 。 当调价幅度为- 时,企业的总收益会达到最大,此时调整后的价格P1= ·P,相应的需求量(销量)Q1=[1- Ed]·Q= ·Q。这里应当注意的是,并非所有企业都能在Q1上组织生产。当企业的生产能力能够达到Q1时,以Q1为产量组织生产,以P1价格出售,达到收益最大;若企业的生产能力Q2不能达到Q1时即,则以Q2为产量组织生产,将Q2代入弹性公式可求得出售价格P2:P2=[ +1]·P 仍然沿用荔枝的例子,通过上述分析,我们可以制定以下价格决策:因为阈值( -1)为- ,则降幅在50%以内可获取更大的收益,如下降20%时,收益会增加120元,降幅超过了50%收益会减少,涨价必定使收益减少;最优调价幅度- 为- ,即价格下降25%降至每千克7.5元时,需求量增加50%增至150千克,取得最大收益1125元;而如果水果商最大进货能力为110千克时(达不到150千克),则他进货110千克荔枝,把价格定在P2= [ +1]·P=9.5元时,取得最大收益1045元。三、需求价格弹性在以总盈利最大为目标的价格决策中的应用 1、企业在获取盈利最大时决策所考虑的因素 许多企业在制定自身的目标时并不一定以总收益最大为目标,而大都以盈利最大为目标,盈利即总收益与总成本之差。若以L表示产品盈利额,Q表示产品销售量,P表示产品价格,V为单位产品变动成本,F为产品的固定成本总额, 则产品盈利额的计算公式为: L=PQ-(QV+F) 一般说来,固定成本总额和单位变动成本在一定时期内是固定不变的。可见,影响盈利额大小的因素是销售量和价格,那么如何取得最大盈利也可以最终归结为价格与需求价格弹性两个因素。 2、盈利达到最大时的最优价格首先根据需求价格弹性公式Ed= 用Q表示价格调整至P3后的需求量Q3,Q3=Q+ P3 Ed-Q Ed,将其代入总盈利函数,可得:L=(P3-V)(Q+ P3 Ed-Q Ed)-FL对P3求一阶导数,Lˊ= Q+(2P3-V) Ed-Q Ed,要使L最大,则要求
Lˊ=0,则P3= (P+V- ),那么企业获取最大盈利时的最优价格P4为 (P+V- ),此时的最佳产量(需求量)Q4= (1-Ed+Ed )。 在这里我们需注意两个问题:其一,单位变动成本V在理论上是不变的, 但在实际中也会有一些变化,如适当的生产量可以套用原材料,节约变动成本,因此在实际定价中应结合具体情况对V进行修正;其二,同样也要考虑到企业的生产能力,当生产能力能达到Q4,那么我们可以在Q4上组织生产和根据最优价格公式定价;当生产能力最大为Q5而不够Q4时,则在Q5上组织生产,并通过需求价格弹性公式推导出此时的定价P5= [ +1]·P。 以上分析可知,需求价格弹性所揭示的经济规律,不仅可以测算企业使得总收益增加的合理调价范围和确定企业获得最大总收益的最优调价幅度,还可以确定盈利最大时的最优的产品价格,为价格调整提供量化依据。企业经营者可以充分利用这些信息,恰当地调整销售价格,以期达到确切的目标和获得最佳的经济效益。当然,需求价格弹性分析,也有局限性和片面性,特别是需求价格弹性数值的衡量标准不同,因此在探讨中应该与其它相关分析方法相结合,以便取得更好的分析效果。
 爱华网
爱华网