德尔菲法简介 作/转载者:贺林 发布时间:2003-4-1 浏览量:869 德尔菲是古希腊地名。相传太阳神阿波罗(Apollo)在德尔菲杀死了一条巨蟒,成了德尔菲主人。阿波罗不仅年轻英俊,而且对未来有很高的预见能力。在德尔菲有座阿波罗神殿,是一个预卜未来的神谕之地,于是人们就借用此名,作为这种方法的名字。
德尔菲法最早出现于50年代末,是当时美国为了预测在其“遭受原子弹轰炸后,可能出现的结果”而发明的一种方法。1964年美国兰德(RAND)公司的赫尔默(Helmer)和戈登(Gordon)发表了“长远预测研究报告”,首次将德尔菲法用于技术预测中,以后便迅速地应用于美国和其他国家。除了科技领域之外,还几乎可以用于任何领域的预测,如军事预测、人口预测、医疗保健预测、经营和需求预测、教育预测等。此外,还用来进行评价、决策和规划工作,并且在长远规划者和决策者心目中享有很高的威望。据《未来》杂志报导,从60年代末到70年代中,专家会议法和德尔菲法(以德尔菲法为主)在各类预测方法中所占比重由20.8%增加到24.2%。80年代以来,我国不少单位也采用德尔菲法进行了预测、决策分析和编制规划工作。
一、德尔菲法的基本特征。德尔菲法本质上是一种反馈匿名函询法。其作法是,在对所要预测的问题征得专家的意见之后,进行整理、归纳、统计,再匿名反馈给各专家,再次征求意见,再集中,再反馈,直至得到稳定的意见。其过程可简单图示如下:匿名征求专家意见——归纳、统计——匿名反馈——归纳、统计……,若干轮后,停止。总之,它是一种利用函询形式的集体匿名思想交流过程。它有区别于其他专家预测方法的三个明显的特点。它们是:匿名性、多次反馈、小组的统计回答。1)匿名性。匿名是德尔菲法的极其重要的特点,从事预测的专家彼此互不知道其他有哪些人参加预测,他们是在完全匿名的情况下交流思想的。
2)多次有控制的反馈。小组成员的交流是通过回答组织者的问题来实现的。它一般要经过若干轮反馈才能完成预测。
3)小组的统计回答。以往,一个小组的最典型的预测结果是反映多数人的观点,少数派的观点至多概括地提及一下。但是这并没有表示出小组的不同意见的状况。
统计回答却不是这样,它报告一个中位数和两个四分点,其中一半落在两个四分点内,一半落在两个四分点之外。这样,每种观点都包括在这样的统计中了,避免了专家会议法酌又一个缺点。中位数和上下四分点的意义,可由下例说明: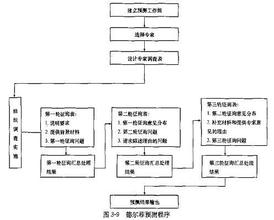
如有13名回答者,对某事件发生时间的预测结果回答如下:1985,1987,1990,1990,1990,1990,1992,1995,1995,1997,1997,2000,永不发生下四分点 中位数 上四分点一般来说,若回答者对某事件发生时间的预测结果回答如下(从小到大排列):x1, x2, x3, ……, xn当n=2k+1时, x中=xk+1, k为整数当n=2k时, x中= (xk+ xk+1)/2上下四分点的奇偶原则,均按类似于上面的原则处理。二、德尔菲法的程序。首先注意,德尔菲法中的调查表与通常的调查表有所不同。通常的调查表只向被调查者提出问题,要求回答。而德尔菲法的调查表不仅提出问题,还兼有向被调查者提供信息的责任。它是专家们交流思想的工具。在德尔菲法过程中,始终有两方面的人在活动:一是预测的组织者;二是被选出来的专家。德尔菲法的程序是以轮来说明的。在每一轮中,组织者与专家都有各自不同的任务。
第一轮:①由组织者发给专家的第一轮调查表是开放式的,不带任何框框,只提出预测问题。请专家围绕预测主题提出预测事件。如果限制太多,会漏掉一些重要事件。②预测组织者要对专家填好的调查表进行汇总整理,归并同类事件,排除次要事件,用准确术语提出一个预测事件一览表,并作为第二轮调查表发给专家。
第二轮:①专家对第二轮调查表所列的每个事件作出评价。例如,说明事件发生的时间、叙述争论问题和事件或迟或早发生的理由。②预测组织者收到第二轮专家意见后,对专家意见作统计处理,整理出第三张调查表。第三张调查表包括:事件、事件发生的中位数和上下四分点,以及事件发生时间在四分点外侧的理由。
第三轮:①把第三张调查表发下去后,请专家做以下事情:重审争论;对上下四分点外的对立意见作一个评价;给出自己新的评价(尤其是在上下四分点外的专家,应重述自己的理由);如果修正自己的观点,也请叙述为何改变,原来的理由错在哪里,或者说明哪里不完善。②专家们的新评论和新争论返回到组织者手中后,组织者的工作与第二轮十分类似:统计中位数和上下四分点;总结专家观点,重点在争论双方的意见。形成第四张调查表。
第四轮:①请专家对第四张调查表再次评价和权衡,作出新的预测。是否要求作出新的论证与评价,取决于组织者的要求。②当第四张调查表返回后,组织者的任务与上一轮的任务相同:计算每个事件的中位数和上下四分点,归纳总结各种意见的理由以及争论点。
注意:①并不是所有被预测的事件都要经过四轮。可能有的事件在第二轮就达到统一,而不必在第三轮中出现。②在第四轮结束后,专家对各事件的预测也不一定都达到统一。不统一也可以用中位数和上下四分点来作结论。事实上,总会有许多事件的预测结果都是不统一的。三、预测结果的表示。德尔菲法的预测结果可用表格、直观图或文字叙述等形式表示。 爱华网
爱华网