第一节 博弈问题概述
一、博弈的基本概念
博弈论(game theory)是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的。换句话说,博弈论研究当某一经济主体的决策既受到其它经济主体决策的影响,而且该经济主体的相应决策又反过来影响到其它经济主体时的决策问题和均衡问题。
在前面几章中,除了寡头市场外,无论是消费者的个人效用函数,还是厂商的利润函数,都只依赖于他自己的选择,而与其他人的选择无关。在这里,经济作为一个整体,各个经济主体的选择是相互影响的。但对于单个的消费者或厂商来说,所有其它经济主体的行为都被包括在一个参数里。这个参数就是价格。除此以外,经济主体在决策时,面临的似乎是一个非人格化的东西。经济主体既不需要考虑他人的选择对自己选择的影响,也何必需要考虑自己的选择对他人的影响。而在本章所介绍的博弈论中,消费者的个人效用函数或厂商的利润函数不仅依赖于自己的选择,而且依赖于具体的某一个或某一些其它经济主体的选择。某一消费者或厂商的最优选择是其它某一些经济主体选择的函数。博弈论的基本概念包括:参与人、行为、信息、战略、支付函数、结果、均衡。参与人是指博弈中选择行动以最大化自身利益(效用、利润等)的决策主体(如个人、厂商、国家)。行动是指参与人的决策变量。战略是指参与人选择行动的规则,它告诉参与人在什么时候选择什么行动。例如,“人不犯我、我不犯人;人若犯我、我必犯人”是一种战略。这里,“犯”与“不犯”是两种不同的行动。战略规定了什么时候选择“犯”,什么时候选择“不犯”。信息是指参与人在博弈中的知识,特别是有关其他参与人(对手)的特征和行动的知识。支付函数是参与人从博弈中获得的效用水平,它是所有参与人战略或行动的函数,是每个参与人真正关心的东西。结果是指博弈者感兴趣的要素的集合。均衡是所有参与人的最优战略或行动的组合。上述概念中,参与人、行动、结果统称为博弈规则。博弈分析的目的是使用博弈规则决定均衡。二、博弈的分类
可以从不同的角度对博弈进行分类。
根据博弈者选择的战略,可以将博弈分成合作博弈(cooperative games)与非合作博弈(non-cooperative games).合作博弈与非合作博弈之间的区别,主要在于博弈的当事人之间能否达成一个有约束力的协议。如果有,就是合作博弈;反之,就是非合作博弈。例如,如果几家寡头通过订立并实行协议,限制产量,制定垄断高价,则称这种博弈为合作博弈。若寡头们在市场竞争中没有达成有约束里的协议,每个企业仅仅是在考虑到竞争对手可能采取的行为的条件下,独立地进行产量与价格的决定,则称这种博弈为非合作博弈。根据参与人行动的先后顺序,可以将博弈分成静态博弈(static game)与动态博弈(dynamic game)。静态博弈是指,博弈中参与人同时选择行动;或者虽非同时行动,但行动在后者并不知道行动在先者采取了什么具体行动。动态博弈是指参与人的行动有先后顺序,而且行动在后者可以观察到行动在先者的选择,并据此作出相应的选择。根据参与人对其他参与人的了解程度,可以将博弈分成完全信息博弈(games of complete information)和不完全信息博弈(games of incomplete information)。完全信息博弈是指:在每个参与人对所有其他参与人(对手)的特征、战略和支付函数都有精确了解的情况下,所进行的博弈。如果了解得不够精确,或者不是对所有的参与人都有精确的了解,在这种情况下进行的博弈就是不完全信息博弈。在以下的几节中,首先介绍非合作博弈,然后介绍合作博弈。而非合作博弈的介绍又分成四种情况分别介绍。这四种情况是:完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈和不完全信息动态博弈。第二节 完全信息静态博弈
一、占优战略均衡
一般来说,由于每个参与人的效用(支付)是博弈中所有参与人的战略的函数,因而每个参与人的最优战略选择依赖于所有其他参与人的战略选择。但在一些特殊的博弈中,一个参与人的最优战略可能并不依赖于其他参与人的战略选择。换句话说,不论其他参与人选择什么战略,他的最优战略是唯一的,这样的最优战略被称为“占优战略”(dominant strategies)。
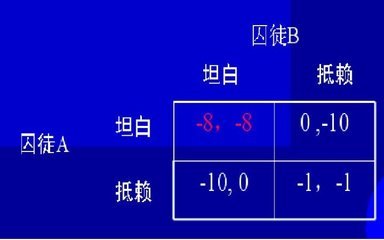
以博弈论中最著名的囚徒困境(prisoner’s dilemma)为例。两个合伙作案的犯罪嫌疑人被抓住了。警方怀疑他们作了许多的案子,但除了其中的一小部分外,警方手中并没有他们作案的确切证据,因而对这两个犯罪嫌疑人犯罪事实的认定及相应的量刑取决于他们自己的供认。假定警方对两名犯罪嫌疑人实行隔离审讯,二者无法订立攻守同盟。同时警方局明确地分别告诉这两名犯罪嫌疑人,他们面临着来以下后果。即如果犯罪嫌疑人与其同伙都供认其全部犯罪事实,那么,由于其罪行的严重性,两人各判8年徒刑。如果某一犯罪嫌疑人供认其全部犯罪事实,而其同伙抵赖,则供认者坦白从宽,从轻判处1年徒刑,而不供认者抗拒从严,从重判处10年徒刑。如果两个犯罪嫌疑人都不供认警方所不知道的犯罪事实。那么,根据已经掌握的证据,只能判处他们每人2年徒刑。表7-1 囚徒困境囚徒B坦白 抵赖
囚徒A 坦白 -8,-8 -1,-10抵赖 -10,-1 -2,-2这两个犯罪嫌疑人所面临的后果可以用表7-1来表示。表中,正数值表示参与人有所得,负数值表示参与人有所失。在表7-1中,每个犯罪嫌疑人都有两种可供选择的战略:坦白或抵赖。但不论同伙选择什么战略,每个犯罪嫌疑人的最优战略是坦白。以犯罪嫌疑人A为例。当犯罪嫌疑人B选择坦白时,A如也选择坦白,则被判处8年徒刑,A如选择抵赖,则将被判处10年徒刑。因而A选择坦白比选择抵赖好。当犯罪嫌疑人B选择抵赖时,A如选择坦白,则被判处1年徒刑,A如选择抵赖,则将被判处2年徒刑。因而A选择坦白还是比选择抵赖好。因此,坦白是犯罪嫌疑人A的占优战略。对于犯罪嫌疑人B来说,坦白同样也是他的占优战略。在博弈中,如果所有的参与人都有占优战略存在,因而博弈将在所有参与人的占优战略的基础上达到均衡,这种均衡称为占优战略均衡。在表7-1中,“A坦白,B也坦白”就是占优战略均衡。应该指出的是,占优战略均衡只要求所有的参与人是理性的,而并不要求每个参与人知道其他参与人也是理性的。因为,不论其他参与人是否理性,占优战略总是一个理性参与人的最优选择。在表7-1中,如果每个犯罪嫌疑人都选择抵赖,则每人将被判处2年徒刑。对于两个犯罪嫌疑人来说,这显然比每人判处8年徒刑要好。但由于AB两人均从个人角度出发,如果不存在某种约束,他们不可能在“A和B一起抵赖”的基础上达到均衡。囚徒困境反映了一个深刻的问题,这就是个人理性与团体理性的冲突。微观经济学的基本观点之一,是可以通过市场机制这只“看不见的手”,在人人追求自身利益最大化的基础上达到全社会资源的最优配置。囚徒困境是对上述基本观点的挑战。二、重复剔除的占优战略均衡
在绝大多数博弈中,占优战略均衡是不存在的。尽管如此,在有些博弈中,我们仍然可以用占优的逻辑找出均衡。
表7-2 按按钮对于吃食量的影响按按钮的猪 吃到的猪食数量大猪 小猪
大猪 4单位 4单位小猪 7单位 1单位两猪同时 5单位 3单位以博弈论中另一个著名的智猪博弈(boxed pigs)为例。猪圈里有两头猪,大猪和小猪。猪圈的一头有一个猪食槽,另一头安装着一个控制着猪食供应的按钮。按一下按钮,将有8个单位的猪食进入猪食槽,供两头猪食用。可供大猪和小猪选择的战略有两种,自己去按按钮,或者等待另一头猪去按按钮。如果某一头猪作出自己去按按钮的选择,它必须付出下列代价:第一,它需要支付相当于2个单位猪食的成本;第二,由于按钮远离猪食槽,它将成为猪食槽边的后到者,从而减少能够吃到的猪食数量。具体情况如表7-2所示。表7-3 智猪博弈小猪按按钮 等待
大猪 按按钮 3,1 2,4等待 7,-1 0,0智猪博弈的后果如表7-3所示。表中的数字表示不同情况下每头猪所吃到的猪食数量减去按按钮的成本之后的净支付水平。表7-3表明,在这个博弈中,无论大猪选择什么战略,小猪的占优战略均为等待。而对大猪来说,其最优战略依赖于小猪的选择。如果小猪选择等待,大猪的最优战略是按按钮;如果小猪选择按按钮,则大猪的最优战略是等待。换句话说,大猪没有占优战略。什么是这一博弈的均衡解呢?假定小猪是理性的,它肯定会选择自己的占优战略——等待。再假定大猪知道小猪是理性的,则大猪会正确地预测到小猪会选择等待,根据小猪的这一选择,大猪选择了在此前提下自己的最优战略——按按钮。在这种情况下大猪和小猪的支付水平分别是2单位和4单位。这是一个多劳不多得、少劳不少得的均衡。在寻找智猪博弈的均衡解时,我们所使用的做法可以归纳如下:首先找出某一博弈参与人的严格劣战略,将它剔除掉,重新构造一个不包括已剔除战略的新的博弈;然后继续剔除这个新的博弈中某一参与人的严格劣战略;重复进行这一过程,直到剩下唯一的参与人战略组合为止。这个唯一剩下的参与人战略组合,就是这个博弈的均衡解,称为“重复剔除的占优战略均衡”(iterated dominance equilibrium).这里所说的劣战略(dominated strategies),是指在其他博弈参与人战略为既定的条件下,某一参与人可能采取的战略中,对自己相对不利的战略。严格劣战略(strictly dominated strategies)则是指:无论其他博弈参与人采取什么战略,某一参与人可能采取的战略中,对自己相对不利的战略。在智猪博弈中,我们首先剔除了小猪的严格劣战略“按按钮”。在剔除掉小猪的这一选择后的新的博弈中,小猪只有等待一个战略,而大猪有两个战略可供选择。我们再剔除新博弈中大猪的严格劣战略“等待”,从而达到重复剔除的占优战略均衡。在现实生活中有许多智猪博弈的例子。例如,在股份公司中,股东承担着监督经理的职能。但不同的股东从监督中得到的收益大小不一样。在监督成本相同的情况下,大股东从监督中得到的收益显然多于小股东。因此,股份公司中监督经理的责任往往由大股东承担,小股东则搭大股东的便车。与前面讨论的占优战略均衡相比,重复剔除的占优战略均衡不仅要求博弈的所有参与人都是理性的,而且要求每个参与人都了解所有的其他参与人都是理性的。在上例中,如果大猪不能排除小猪按按钮的可能性,按按钮就不一定是大猪的最优选择。三、纳什均衡
纳什均衡(Nash equilibrium)是指这样一种均衡。在这一均衡中,每个博弈参与人都确信,在给定其他参与人战略策略决定的情况下,他选择了最优战略。纳什均衡是完全信息静态博弈解的一般情况。构成纳什均衡的战略组合一定是在重复剔除严格劣战略过程中无法被剔除的战略组合。
在占优战略均衡中,无论所有其他参与人选择什么战略,一个参与人的占优战略都是他的最优战略。显然,这一占优战略也必定是所有其他参与人选择某一特定战略时该参与人的最优战略。因此,占优战略均衡一定是纳什均衡。在重复剔除的占优战略均衡中,最后剩下的唯一战略组合,一定是在重复剔除严格劣战略过程中无法被剔除的战略组合。因此,重复剔除的占优战略均衡也一定是纳什均衡。表7-4 性别战女方看足球 逛商店
男方 看足球 3,1 0,0逛商店 0,0 1,3纳什均衡所包括的情况远不止占优战略均衡和重复剔除的占优战略均衡。以博弈论中经常提到的性别战(battle of the sexes)为例。谈恋爱中的男女通常是共渡周末而不愿意分开活动的。但对于周末干什么,男女双方各自有着自己的偏好。男方喜欢看足球比赛,女方喜欢逛商店。不同选择下男女双方的得失见表7-4。在这个博弈中,存在着两个纳什均衡。男女双方或者一起去看足球,或者一起去逛商店。如果没有进一步的信息,我们无法确定男女双方在上述博弈中会作出什么选择。与重复剔除的占优战略均衡一样,纳什均衡不仅要求博弈的所有参与人都是理性的,而且要求每个参与人都了解所有的其他参与人都是理性的。第三节 完全信息动态博弈
一、子博弈精炼纳什均衡
在动态博弈中,参与人的行动有先后顺序,而且后行动的参与人在自己行动之前可以观测到先行动者的行动,并选择相应的战略。由于先行动者拥有后行动者可能选择战略的完全信息,因而先行动者在选择自己的战略时,就可以预先考虑自己的选择对后行动者选择的影响,并采取相应的对策。
表7-5 房地产开发博弈(静态)B开发 不开发A 开发 -3,-3 1,0不开发 0,1 0,0以某一房地产开发博弈为例,表7-5显示了静态条件下双方参与人的得失。房地产开发商A是先行动者。在行动之前,A对竞争者B的战略进行了预测。在行动开始前的A看来,如果不计得失,B有四种战略可选择。第一,无论A是否开发,B都要开发。第二,如果A开发,B也开发;如果A不开发,B也不开发。表7-6 A对B的预测B开发,开发 开发,不开发 不开发,开发 不开发,不开发
A 开发 -3,-3 -3,-3 1,0 1,0不开发 0,1 0,0 0,1 0,0第三,如果A开发,B就不开发;如果A不开发,B就开发。第四,无论A是否开发,B必定不开发。将B可能采取的选择与表7-5中博弈双方相应选择的得失结合起来,可以得出表7-6。在表7-5中,存在着两个纳什均衡,即(A开发,B不开发)和(A不开发,B开发)。而在B可能选择的战略中,战略一虽然包括了上述后一种纳什均衡,但没有包括前一种纳什均衡;战略四虽然包括了上述前一种纳什均衡,但没有包括后一种纳什均衡;至于战略二,则上述两种纳什均衡都没有包括;只有战略三包括了上述两种纳什均衡。换句话说,如果B选择战略三,那么,不论A作出什么选择,B的回应都达到纳什均衡。而在给定B会采取战略三(即如果A开发,B就不开发;如果A不开发,B就开发)来回应A的选择的前提下,开发是A的占优战略。因而A选择了开发。以上的分析方法,称为子博弈精炼纳什均衡(sub-game perfect Nash equilibrium)。子博弈是原博弈的一部分,它本身可以作为一个独立的博弈进行分析。例如,在表7-5中,每一列或每一行都是一个子博弈。任何博弈本身则被称为自身的一个子博弈。只有当某一战略组合在每一个子博弈(包括原博弈)上都构成一个纳什均衡,这一战略组合才是子博弈精炼纳什均衡。仍然以前面提到的房地产开发博弈为例,这里涉及到包括原博弈在内的三个子博弈。由于A是先行动者,那么,在A选择了开发之后,B的回应构成了子博弈甲,如表7-5的第一行,这里的纳什均衡是A开发,B不开发。在A选择了不开发之后,B的回应也构成了子博弈乙,如表7-5的第二行,这里的纳什均衡是A不开发,B开发。而整个表7-5,则表示A在有可能选择开发或不开发的情况下,B的回应。它既是原博弈,又是自身的子博弈。这里存在着本段中提到的两个纳什均衡。而前面提到的B的四种战略中,只有战略三在子博弈甲、乙中都构成纳什均衡,其它的战略至少在子博弈甲、乙之一中不构成纳什均衡,因而这一博弈中唯一的子博弈精炼纳什均衡,就是(开发,{不开发,开发}),即作为后行动者的B选择战略三,而作为先行动者的A选择开发。就特定情况而言,除了(开发,{不开发,开发})之外,参与人也可以选择其它战略。在上述房地产开发博弈中,在A选择开发时,无论B选择战略三还是战略四(即,无论A是否开发,B必定不开发),其结果——A开发,B不开发——都是构成纳什均衡的。而子博弈精炼纳什均衡方法所要剔除的,正是这种只在特定情况下是合理的,而在其它情况下不合理的战略组合。二、重复博弈
以上讨论的动态博弈有这样一个特点。这就是,参与人在前一个阶段的选择将决定随后的子博弈的结构。在上述房地产开发博弈中,子博弈甲不同于子博弈乙。当A选择了开发后,子博弈乙就被排除了。这样的动态博弈称为序贯博弈(sequential games)。动态博弈中另外一类是所谓的重复博弈(repeated games)。顾名思义,重复博弈是指同样结构的博弈重复许多次,其中的每次博弈称为阶段博弈(stage game)。
影响重复博弈均衡结果的主要因素,是博弈重复的次数和信息的完备性。重复次数的重要性来自参与人在短期利益和长期利益之间的权衡。当博弈只进行一次时,每个参与人都只关心一次性的支付;但如果博弈重复多次,参与人可能会为了长远利益而牺牲眼前利益,从而选择不同的均衡战略。就信息的完备性而论,当一个参与人的支付函数还不为其他参与人所知时,该参与人可能有积极性建立一个良好的声誉以换取长远利益。在这里,我们只讨论博弈重复的次数。表7-7 产品定价博弈B低价 高价
A 低价 24,24 40,8高价 8,40 32,32我们用一个产品定价博弈的例子来分析重复博弈。表7-7显示了这一博弈的有关情况。该表表明,在一次性的完全信息静态博弈中,两个参与人A与B均有占优战略,占优战略均衡为双方都定低价。而一次性博弈意味着没有人能够对其他参与人的行为进行奖励或报复。而在动态的重复博弈中,所有参与人过去的行为都是观测得到的,因而某一参与人可以通过自己在本阶段博弈中的选择,来回应其他参与人在以前的阶段博弈中的行为。以产品定价博弈为例。如果上一次阶段博弈中,B选择了高价,使得也选择了高价的A得到了好处,那么A可以在本阶段博弈中继续选择高价作为对B的奖励。如果在上一次阶段博弈中,B选择了低价,使得选择了高价的A受到了损失,那么A可以在本阶段博弈中选择低价作为对B的报复。博弈重复的次数对参与人的选择有什么样的影响呢?我们分两种情况来讨论。先看博弈重复次数无限时的情况。以表7-7所举的产品定价博弈为例。如果B选择与A合作维持产品高价,则B各阶段所得是(32,32,32,32...);如果B选择不与A合作,并在第一阶段通过选择低价使得选择高价的A受到损失,A则在以后各阶段的博弈中选择低价以报复,则B各阶段所得为(40,24,24,24...)。换句话说,B在第一高等博弈中因不与A合作而得到的额外好处,将因为A在以后各阶段所采取的报复性选择而抵消。重复博弈若干次后,B的不合作态度将导致得不偿失的后果。在这里,A所采取的战略称为冷酷战略(grim strategies)。按照这种战略,A起初选择合作;但如果B在某一阶段博弈中选择不合作的话,A将永远选择不合作。A这样做的理由是:选择不合作(低价),他各阶段的所得是24;而选择合作(高价),他各阶段的所得少于24,因为B在某一阶段博弈中的不合作排除了双方合作获得双赢的可能。因此,A有坚持冷酷战略的积极性。而B为了减少损失,也就只能一直不合作下去。换句话说,冷酷战略意味着任何一个参与人的一次性不合作将触发永远的不合作。在这种情况下,重复博弈的所有参与人慑于冷酷战略的严重后果,有积极性维持合作。再看博弈重复次数有限时的情况。博弈重复次数有限,意味着存在所有参与人都可以预测到的“最后一次”。在最后的阶段博弈中,如果某一参与人选择了自己的占优战略,给其他参与人造成损失,则其他参与人不可能报复。所有的参与人都明白这一点,因而在最后一次阶段博弈中都会选择占优战略——给自己的产品制定低价,从而构成与完全信息静态博弈相同的占优战略均衡。所有参与人在最后阶段博弈中都会不约而同地选择低价战略,这意味着无论B在倒数第二阶段——即最后阶段以前的那个阶段——博弈中采取什么战略,A在最后阶段都将采取低价战略。因此,在倒数第二阶段中,B就没有必要因为担心A的报复而采取高价战略。换句话说,在给定最后阶段所有参与人都会选择占优战略的前提下,所有的参与人在倒数第二阶段的博弈中也都会选择占优战略。由此从最后的阶段开始,逐个阶段进行推理,可以得出以下结论:在阶段博弈有唯一的纳什均衡时,n次重复博弈的唯一子博弈精炼纳什均衡结果,是阶段博弈的纳什均衡重复n次。这就是说,每个阶段博弈出现的都是一次性博弈的均衡结果。在这里,阶段博弈纳什均衡的唯一性是一个重要条件。如果纳什均衡 是唯一的,上述结论就不一定成立。三、动态博弈战略行动
在动态博弈中,参与人为了使得其他参与人的选择对自己有利,往往采取一些行动来影响其他参与人对于自己行为的预期。这些行为称为战略行动(strategic move)。
以下是一些战略行动的例子。1.首先行动优势首先行动优势(first-mover advantage)是指,在博弈中首先作出战略选择并采取相应行动的参与人可以获得较多的利益。例如,在前面提到的性别战中,存在着两个纳什均衡,即两人一起看足球比赛或逛商店。男方偏好看足球比赛,而女方偏好逛商店。在这种情况下,男方仅仅提出要看足球比赛是不够的,他应该采取行动,先买好足球票。从而使女方因感到“男朋友十分想看这场比赛”或因感到“买球票不容易,不看可惜”而接受两人一起看足球比赛的选择。2.确实可信的威胁表7-8 房地产开发博弈(B承诺后)B开发 不开发A 开发 -3,-3 1,-5不开发 0,1 0,-5确实可信的威胁(credible threat)是指,博弈的参与人通过某种行动改变自己的支付函数,从而使得自己的威胁显得可信。参与人为改变博弈结果而采取的措施称为承诺(commitment)。表7-9 A对B的预测(B承诺后)B开发,开发 开发,不开发 不开发,开发 不开发,不开发A 开发 -3,-3 -3,-3 1,-5 1,-5不开发 0,1 0,-5 0,1 0,-5我们再来看前面提到过的房地产开发博弈。在这一例子中,B所选择的战略一(无论A是否开发,B都要开发)之所以不是子博弈精炼纳什均衡,是因为存在着如同表7-5和表7-6所表示的支付函数。如果A在作出选择之前,B与某一客户签订合同,规定B在一定期限内向客户交付一定面积的住房,如果B不能按时履约,则赔偿客户5单位货币。有了这样一个承诺,表7-5就变成表7-8,在完全信息静态博弈下,B就有了占优战略——开发。因而B的第一种战略——无论A是否开发,我都要开发——就成为确实可信的威胁。表7-6就变成表7-9,因而这一博弈的子博弈精炼纳什均衡,也就从原来的(开发,{不开发,开发})变成现在的(不开发,{开发,开发})。第四节 不完全信息静态博弈
前面介绍的博弈都包含一个基本假设,即完全信息假设。按照这一假设,每个参与人对所有其他参与人(对手)的类型、战略和支付函数都有精确的了解。但是,在许多情况下,参与人对对手的了解往往是不够精确的。这种情况下的博弈就是不完全信息博弈。
表7-10 市场进入博弈A高成本 低成本默许 阻挠 默许 阻挠
B 进入 40,50 -10,0 30,100 -10,140不进入 0,300 0,300 0,400 0,400举例来说,某一市场原来被A企业所垄断。现在B企业考虑是否进入。B企业知道,A企业是否允许它进入,取决于A企业阻挠B企业进入所花费的成本。如果阻挠的成本低,那么,正如表7-10后两列所表示的,A企业的占优战略是阻挠,博弈有重复剔除的占优战略均衡——A阻挠,B不进入。如果阻挠的成本高,那么,正如表7-10前两列所表示的,A企业的占优战略是默许B进入,博弈有重复剔除的占优战略均衡——A默许,B进入。B企业所不知道的,是A企业的阻挠成本是高是低。这里,某一参与人本人知道、其他参与人则不知道的信息称为私人信息。某一参与人所拥有的全部私人信息称为他的类型。在上述例子中,阻挠成本就是A的私人信息。高阻挠成本和低阻挠成本则是两种不同的类型。显然,在这里,B所遇到的,是不确定性条件下的选择问题。因为B不仅不知道A的类型(是高还是低),而且不知道不同类型的分布概率。解决这类问题的方法之一,就是把不确定性条件下的选择转换为风险条件下的选择。在风险条件下,B虽然不知道A的类型,但可以知道不同类型的分布概率。将不确定性条件下的选择转换为风险条件下的选择,称为海萨尼转换(the Harsanyi transformation)。按照海萨尼的方法,所有参与人的真实类型都是给定的。其他参与人虽然不清楚某一参与人的真实类型,但知道这些可能出现的类型的分布概率,而且这种概率是公共知识。用上例来说,公共知识不仅意味着B企业知道A企业高阻挠成本与低阻挠成本的分布概率,而且意味着A也清楚B知道这一概率。通过海萨尼转换,不完全信息博弈变成了完全但不完美信息博弈(games of complete but imperfect information)。这里的不完美信息,就是指其他参与人只知道某一参与人某些方面类型的分布概率,而不知道该参与人在这些方面的真实类型。在上述转换的基础上,海萨尼提出了贝叶斯纳什均衡(Bayesian Nash equilibrium)。对此,可以作如下解释:在不完全信息静态博弈中,参与人同时行动,没有机会观察到别人的选择。给定其他参与人的战略选择,每个参与人的最优战略依赖于自己的类型。由于每个参与人仅知道其他参与人有关类型的分布概率,而不知道其真实类型,因而,他不可能知道其他参与人实际上会选择什么战略。但是,他能够正确地预测到其他参与人的选择与其各自的有关类型之间的关系。因此,该参与人的决策目标就是:在给定自己的类型,以及给定其他参与人的类型与战略选择之间关系的条件下,使得自己的期望效用最大化。贝叶斯纳什均衡是一种类型依赖型战略组合。在给定自己的类型和其他参与人类型的分布概率的条件下,这种战略组合使得每个参与人的期望效用达到了最大化。回到上面提到的市场进入的例子。在这个例子里,对于挑战者B来说,原垄断者A在阻挠成本方面,存在着两种可能性:高成本或低成本。B不知道A的阻挠成本究竟是高是低,但他知道A在这两种不同阻挠成本下会作出的选择,以及不同阻挠成本(类型)的分布概率。假定高成本的概率为x,则低成本的概率为(1-x)。如果A的阻挠成本高,A将默许B进入市场;如果A的阻挠成本低,A将阻挠B进入市场。在这两种情况下,如表7-10所示,B进入的支付函数分别是得到40和失去10。因此,B选择进入所得到的期望利润为40x+(-10)(1-x),选择不进入的期望利润为0。简单的计算表明,当A阻挠成本高的概率大于20%时,挑战者B选择进入得到的期望利润大于选择不进入的期望利润。此时,选择进入是B的最优选择。此时的贝叶斯纳什均衡为,挑战者B选择进入,高成本原垄断者选择默许,低成本原垄断者选择阻挠。第五节 不完全信息动态博弈
在动态博弈中,行动有先后次序,后行动者可以通过观察先行动者的行为,来获得有关先行动者的信息,从而证实或修正自己对先行动者的判断。
如上所述,在不完全信息条件下,博弈的参与人知道其他参与人可能有哪几种类型,也知道不同的类型与相应战略选择之间的关系。但他们并不知道其他参与人的真实类型。在不完全信息静态博弈中,我们是通过海萨尼转换,即通过假定其他参与人知道某一参与人的所属类型的分布概率,来得出博弈的贝叶斯纳什均衡结果的。而在不完全信息动态博弈中,问题变得更加简单。博弈开始时,某一参与人既不知道其他参与人的真实类型,也不知道其他参与人所属类型的分布概率。他只是对这一概率分布有自己的主观判断,即有自己的信念。博弈开始后,该参与人将根据他所观察到的其他参与人的行为,来修正自己的信念。并根据这种不断变化的信念,作出自己的战略选择。对应于不完全信息动态博弈的均衡概念是精炼贝叶斯均衡(perfect Bayesian equilibrium)。这个概念是完全信息动态博弈的子博弈精炼纳什均衡与不完全信息静态均衡的贝叶斯(纳什)均衡的结合。具体来说,精炼贝叶斯均衡是所有参与人战略和信念的一种结合。它满足如下条件:第一,在给定每个参与人有关其他参与人类型的信念的条件下,该参与人的战略选择是最优的。第二,每个参与人关于其他参与人所属类型的信念,但是使用贝叶斯法则从所观察到的行为中获得的。贝叶斯法则是概率统计中的应用所观察到的现象对有关概率分布的主观判断(即先验概率)进行修正的标准方法。采用上一节的例子,可以将贝叶斯规则的分析思路表达如下。挑战者B不知道原垄断者A是属于高阻挠成本类型还是低阻挠成本类型,但B知道,如果A属于高阻挠成本类型,B进入市场时A进行阻挠的概率是20%(此时A为了保持垄断带来的高利润,不计成本地拼命阻挠);如果A属于低阻挠成本类型,B进入市场时A进行阻挠的概率是100%。博弈开始时,B认为A属于高阻挠成本企业的概率为70%,因此,B估计自己在进入市场时,受到A阻挠的概率为:0.7×0.2+0.3×1=0.44
0.44是在B给定A所属类型的先验概率下,A可能采取阻挠行为的概率。当B进入市场时,A确实进行阻挠。使用贝叶斯法则,根据阻挠这一可以观察到的行为,B认为A属于高阻挠成本企业的概率变成A属于高成本企业的概率=0.7(A属于高成本企业的先验概率)×0.2(高成本企业对新进入市场的企业进行阻挠的概率)÷0.44=0.32根据这一新的概率,B估计自己在进入市场时,受到A阻挠的概率为:0.32×0.2+0.68×1=0.744如果B再一次进入市场时,A又进行了阻挠。使用贝叶斯法则,根据再次阻挠这一可观察到的行为,B认为A属于高阻挠成本企业的概率变成A属于高成本企业的概率=0.32(A属于高成本企业的先验概率)×0.2(高成本企业对新进入市场的企业进行阻挠的概率)÷0.744=0.086这样,根据A一次又一次的阻挠行为,B对A所属类型的判断逐步发生变化,越来越倾向于将A判断为低阻挠成本企业了。以上例子表明,在不完全信息动态博弈中,参与人所采取的行为具有传递信息的作用。尽管A企业有可能是高成本企业,但A企业连续进行的市场进入阻挠,给B企业以A企业是低阻挠成本企业的印象,从而使得B企业停止了进入地市场的行动。应该指出的是,传递信息的行为是需要成本的。假如这种行为没有成本,谁都可以效仿,那么,这种行为就达不到传递信息的目的。只有在行为需要相当大的成本,因而别人不敢轻易效仿时,这种行为才能起到传递信息的作用。传递信息所支付的成本是由信息的不完全性造成的。但不能因此就说不完全信息就一定是坏事。研究表明,在重复次数有限的囚徒困境博弈中,不完全信息可以导致博弈双方的合作。理由是:当信息不完全时,参与人为了获得合作带来的长期利益,不愿过早暴露自己的本性。这就是说,在一种长期的关系中,一个人干好事还是干坏事,常常不取决于他的本性是好是坏,而在很大程度上取决于其他人在多大程度上认为他是好人。如果其他人不知道自己的真实面目,一个坏人也会为了掩盖自己而在相当长的时期内做好事。
 爱华网
爱华网