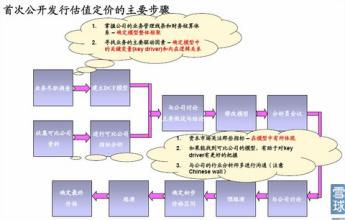
一、股权自由现金流与红利
公司每年不仅需要偿还一定的利息或本金,同时还要为其今后的发展而维护现有的资产、购置新的资产。当我们把所有这些费用从现金流入中扣除之后,余下的现金流就是股权自由现金流(FCFE)。FCFE的计算公式为:
FCFE=净收益 + 折旧 - 资本性支出 - 营运资本追加额 - 债务本金偿还 + 新发行债务
FCFE是公司能否顺利支付红利的一个指标。有一些公司奉行将其所有的FCFE都作为红利支付给股东的政策,但大多数公司都或多或少地保留部分股权自由现金流。FCFE之所以不同于红利,其原因有以下几条:
红利稳定性的要求。一般来说公司都不愿意变动红利支付额。而且因为红利的流动性远小于收益和现金流的波动性。所以人们认为红利具有粘性。
未来投资的需要。如果一个公司预计其在将来所需的资本性支出会有所增加,那么它就不会把所有的FCFE当作红利派发给股东。由于新发行股票的成本很高,公司往往保留一些多余的现金并把它作为满足未来投资所需资金的来源。
税收因素。如果对红利征收的所得税税率高于资本利得的税率,则公司会发放相对较少的红利现金。并把多余的现金保留在企业内部。
信号作用。公司经常把红利支付额作为其未来发展前景的信号:如果红利增加。则公司前景看好:如果红利下降,则公司前景黯淡。
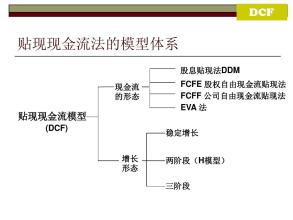
二、稳定增长(一阶段)FCFE模型
如果公司一直处于稳定增长阶段,以一个不主烃的比率持续增长,那么这个公司就可以使用稳定增长的FCFE模型进行估价。
在稳定增长模型中股权资本的价值是三个变量的函数:下一年的预期FCFE、稳定增长率和投资者的要求收益率:
P0 = FCFE1/(r – gn)
其中:P0=股票当前的价值
FCFE1=下一年预期的FCFE
r=公司的股权资本成本(亦是投资者的要求收益率)
gn=FCFE的稳定增长率
这个模型的前提假设与Gordon增长模型非常相似,因此它在应用方面也面临着同样的限制条件。模型中使用的增长率必须是合理的。它与公司所处的宏观经济环境的发展速度有关系。作为一种通用规则,公司的稳定增长率不会超过其所处的宏观经济增长率1——2个百分点以上。
公司处于稳定状态的假设也说明了公司必须具备的其他维持稳定增长所需的条件。比如说:不允许公司的资本性支出远远大于折旧额:公司的资产也必须具有市场平均风险(如果应用CAPM模型,那么公司股权的β值应与1相差不大)。一家公司要能够实现稳定增长,就必须具备下面两个特征:
(a)折旧能够完全弥补资本性支出。
(b)股票的 值为1。如果应用其他模型来估计公司的股权资本成本,那么其结果与市场全部股票的平均股权资本成本相接近。
3、模型的适用性
像Gordon增长模型一样,这个模型非常适用于那些增长率等于或者稍低于名义经济增长率的公司。当然,它相对于红利增长模型有了很大改进,因为那些稳定增长的公司有时会支付比FCFE高得多的红利,有时支付的红利运远远小于FCFE。注意,如果公司处于稳定增长阶段,而且其支付的红利与FCFE始终保持一致,那么通过此估价模型得到的公司价值与Gordon增长模型计算出的结果是相同的。
三、两阶段FCFE模型
FCFE两阶段估价模型适用于那些预计会在一定时间段里快速增长,然后再进入稳定增长阶段的公司。
股票的价值由两部分组成:一是超常增长时期每年FCFE的现值,二是超常增长时期结时期末价值的现值。
股票价值 = 高速增长阶段FCFE的现值 + 期末价值现值
= ∑FCFEt/(1 + r) + Pn/(1+r)n
其中:FCFEt=第t年的FCFE
Pn=高速增长阶段期末的股票价格
r=高速增长阶段内股权投资者的要求收益率
期末价值Pn一般使用永续稳定增长模型来计算。
Pn=FCFEt+1/(rn-gn)
其中:gn=第二阶段稳定增长阶段的增长率
rn=稳定增长阶段内股权投资者的要求收益率。
在应用稳定增长模型的时候,我们仍然应该考虑在上一节中提到过的注意事项,另外,我们在估计高速增长阶段期末FCFE的时候,往往已经使用了对第一阶段的假定,因此这些假定也应与稳定增长阶段的假设相一致。比如说,公司在超常增长阶段内的资本性支出可能会远远大于折旧,但当公司进入稳定增长阶段后,二者之间的差距应该减小。
这个模型的假设条件与两阶段红利贴现模型是一样的。顾名思义,两阶段就是指公司在前一时期可以较高的速度增长,然后立即进入稳定增长阶段。此模型的不同点就是用FCFE代替了红利。当然,它比红利贴现模型给出了更好的结果,特别是对于那些当前支付的红利并不能长久维持的公司(因为红利要高于FCFE),和红利支付额小于其承受能力的公司(红利少于FCFE)。
四、E模型——三阶段的FCFE模型
E模型适用于那些要经历三个不同增长阶段的公司。三阶段一般是:起初的高增长阶段、增长率下降的过渡阶段和增长率保持不变的稳定阶段。
E模型计算了全部三个增长阶段预期FCFE的现值。
P0 = ∑FCFEt/(1+r)t + ∑FCFEt/(1+r)t + Pn2/(1+r)n
t从1至n1 t从n1+1至n2
其中:P0=当前股票的价值
FCFEt=第t年的FCFE
r=股权资本成本
Pn2=过渡阶段期末股票的价值=FCFEn2+1(r-gn)
n1=高速增长阶段的结束时间
n2=过渡阶段的结束时间
由于模型假定了公司的增长速度会经历三个不同的阶段:高速增长、过渡和稳定增长,所以其他变量的假定都必须与这一增长率的假设相一致,这一点尤为重要。
资本性支出和折旧。当公司从高速增长阶段过渡到稳定增长阶段的时候,其资本性支出与折旧的关系自然也会改变。在高速增长阶段,资本性支出可能会比折旧大得多;而在过渡阶段,二者之间的差距应该逐步缩小;在稳定增长阶段,资本性支出和折旧应该大致持平。
风险。随着公司增长率的改变,它的风险持性也会随之改变。在CAPM模型中,随着增长速度的下降,公司的β值总会趋向干1,这一点已经得到了实证研究的确认。
由于模型中公司有三个增长阶段,而且从高增长阶段过渡到稳定增长阶段有一个渐进的过程,所以它特别适合于那些当前具有很高增长率的公司的估价。模型中关于公司发展速度的假定与三阶段红利贴现模型相似,唯一不同是我们使用的是FCFE(而不是红利)。应用此模型可以保证那些红利支付额远远高于或低于其FCFE的公司的估价更为准确。
 爱华网
爱华网